In the last decade, the value of the discrete ordinates method of solving the linear Boltzmann transport equations (LBTEs) as a means of absorbed dose calculation in radiotherapy has been widely appreciated (Gifford et al 2006, Vassiliev et al 2010, Bedford 2019). Compared to Monte Carlo simulation, which is an alternative method of solving the LBTE, the discrete ordinates method is deterministic and therefore provides solutions in which stochastic uncertainty is absent (Vassiliev 2017). The Acuros implementation (Varian Medical Systems, Palo Alto, CA) has also led to the widespread application in many centres, together with numerous comparisons with Monte Carlo simulation (Han et al 2011, 2013, Fogliata et al 2012, Hoffmann et al 2018). The inclusion of a magnetic field in the physical modelling has enabled application to MR-guided radiotherapy (St Aubin et al 2015, 2016, Zelyak et al 2018a, 2018b).
However, the method has much greater potential for application in radiotherapy than has so far been realised. Two particular impediments to its application can be identified, notably (a) the difficulty of applying it to proton therapy, and (b) the difficulty of its application to inverse planning. In the former, that of application to proton therapy, the difficulty is that proton transport is largely unidirectional, with relatively little energy loss until the Bragg peak, where the particles change direction considerably, and lose all of their remaining energy. Modelling this process using LBTE without any prior assumptions such as continuous slowing down approximation requires many energy and direction ordinates, most of which, for the initial part of the beam trajectory, are irrelevant, and a drain on memory resources (Sanchez and McCormick 2004, Uilkema 2012).
With regard to the latter impediment, that of inverse planning, one of the advantages of the discrete ordinates method is that the absorbed dose due to all control points of all beams can be calculated by one solution of the transport equations. This is efficient for volumetric modulated arc therapy (VMAT), where there are many control points, but a difficulty arises with inverse planning, where the dose distribution due to each fluence element, or bixel, of each beam is invariably required for the inverse planning algorithm. This can be accomplished by the discrete ordinates method by repeated applications, but is very inefficient.
The ultimate aim of the project described in this paper is to address these issues so as to provide a discrete ordinates solver which can be used for proton therapy and also applied efficiently to inverse planning. For proton therapy, the approach is to treat the initial highly directional proton trajectory as a fixed source based on semi-empirical methods, mostly reserving the discrete ordinates solution for the Bragg peak. With inverse planning, the approach is to use the discrete ordinates method to perform regular calculations of the dose due to the entire plan, thereby utilising the efficiency of the method, and then to use a convolution method to provide the bixel-based doses required for inverse planning purposes. Compatibility of the LBTE solver with the convolution method is therefore required. For all of these methods, a short computation time and a reasonable memory allocation are needed, and it is therefore necessary to make some simplifications to produce a practical solution. The main simplification, compared to the Acuros implementation (Vassiliev et al 2010), is to use fewer directional and energy ordinates in the quadrature.
As this project is substantial, it is not feasible to present all of the work in one paper. This paper therefore concentrates on the methods and validation of Boltzmann solutions with both photon and proton beams. Actual incorporation of the methods into inverse planning is not described, although this goal is in the background throughout. The form of the paper is consequently as follows: the Boltzmann solver is described firstly for photon beams and then for proton beams. The adequacy of the iterative scheme and the quadrature is demonstrated for homogeneous media. The method is then applied to a lung case, where the tissue inhomogeneity is particularly pronounced. In this case, photon arcs (VMAT), fixed (passively scattered) proton beams and proton arcs are used. The results when using the Boltzmann approach are compared with those produced by alternative algorithms already implemented in the inverse planning context.
2.1. Head modelThe LBTE solver proceeded by projecting unscattered photons or protons into the patient model. In the case of photons, the fluence was calculated using a dual-source model of a Versa HD linear accelerator (Elekta AB, Stockholm) with a source-axis distance of 1000 mm (Bedford et al 2013). A 6 MV flattened beam was considered in this work, although the approach can also be used for a flattening filter-free beam. For each of the two radiation sources in the dual-source model, representing primary photons and head scatter, divergent rays were traced throughout the patient model according to a regular Cartesian grid defined at the isocentric plane (Siddon 1985, Bedford et al 2022). The intensities of the rays were determined from the off-axis position of the rays according to a lookup table defined in the beam data for the dose calculation model (Bedford 2002). A fluence grid at the position of the collimating device was defined for each source in the model and the contributions of the rays to the elements of the fluence map were determined, taking into account the divergence of the rays. The resulting fluence was then convolved with a Gaussian source function of specified intensity and width, again determined as part of the beam data. For the Versa HD accelerator, the primary source was modelled as having a width (standard deviation) of 0.8 mm and a length of 1.0 mm, while the secondary source, at 150 mm from the primary source, was modelled as having a width and length of 18.0 mm. Further details of the source model are given elsewhere (Bedford et al 2022).
In the case of passively scattered protons, the same source model was used, but with parameters representing the 230 MeV beam of a double-scattering system (Ion Beam Applications S.A., Louvain-la-Neuve, Belgium) (Slopsema 2012), with a single source having a source-axis distance of 2300 mm. The width and length of the source were both modelled as 30.0 mm (Slopsema et al 2014). For proton arcs, the pencil beam width (two standard deviations) was taken as 10.0 mm.
2.2. QuadratureThe angular quadrature for discrete ordinates was based upon the IEC61217 convention for gantry and couch angles, so that the different discrete directions could be conveniently addressed using the corresponding beam orientations. The 'gantry angles' of the quadrature were 0.0°, 47.5°, 90.0°, 132.5°, 180.0°, 227.5°, 270.0° and 312.5°, i.e. approximately 45° spacing, with a bias of the diagonal directions of 2.5° towards the lateral directions. The 'couch angles' were spaced at 45° from 270° to 45° through 0°. The couch angles, c, and gantry angles, g, were considered as a spherical coordinate system, with each combination of c and g giving a direction vector, Ω:
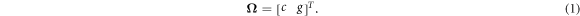
This range of gantry and couch angles permitted the complete orientation space to be addressed, corresponding to the arrangement of lines of latitude and longitude around the globe (figure 1). This was useful for visualisation purposes, but had the drawback that the solid angle occupied by each orientation varied between the ordinates, reducing towards the orientations with gantry 0° and 180°. At these two orientations, the variation of the couch angles led to multiple ordinates at identical orientation. The couch angles of the ordinates at gantry 0° and 180° were therefore constrained to 0°. A simple uniform weighting was used for the angular quadrature, the small bias of the diagonal gantry angles towards 90° or 270° being used to ensure even coverage of the orientation space. For an ordinate with couch angle c and gantry angle g, the weighting was given by:
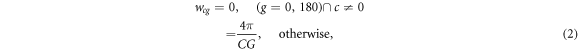
where C (=4) and G (=8) represented the total number of couch and gantry angles in the quadrature. For Compton scattering of photons, an additional weighting factor was used, which is described in section 2.3. Note that the angular quadrature was fixed in space and used for all segments of the VMAT arcs, so that a single application of the LBTE could be used to calculate dose for the complete plan, with maximum efficiency.
Figure 1. Illustration of the angular quadrature used in this work. The set of directions shown in the transaxial view is repeated at the four angles in the coronal view, thereby covering the 4π steradians of direction space.
Download figure:
Standard image High-resolution imageEnergy was discretised into G groups (g = 1, 2, 3, ..., G) using the multigroup method (Lewis and Miller 1984). Each group was characterised by a discrete energy, Eg
. For photons, the energy quadrature was arranged such that Eg
increased in 0.5 MeV steps up to 4.0 MeV, followed by 1.0 MeV steps up to 10.0 MeV. For protons, the energy quadrature was arranged in 5 MeV steps from 5 to 250 MeV. The uppermost energies for both photons and protons were redundant, but were included for generality, should higher energy particles need to be considered. The group boundaries lay midway between the discrete energies, Eg
, with the upper boundary for group g being  and the lower energy boundary being
and the lower energy boundary being  As in previous work (Gifford et al
2006), the continuous fluence
As in previous work (Gifford et al
2006), the continuous fluence  where Ω referred to the angular ordinate, was divided into a fluence component and an energy component:
where Ω referred to the angular ordinate, was divided into a fluence component and an energy component:
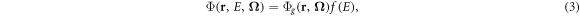
with  then being selected to be constant within each energy range:
then being selected to be constant within each energy range:
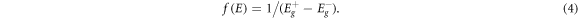
Note that a consequence of this was that the total fluence for group g, as given by the integral  was simply equal to
was simply equal to  which simplified the computational handling of the energy quadrature.
which simplified the computational handling of the energy quadrature.
The differences between transport of photons and protons in the LBTE solver were mostly found in the initial transport of unscattered fluence, and they are therefore outlined separately. With regard to photons, for each ray cast from the head model, equivalent path length was determined, from which an exponential decay was calculated. The energy for this was calculated from an energy spectrum and the attenuation coefficients were taken from ICRU46 (International Commission on Radiation Units and Measurements 1992). Taking the position in the beam's eye view to be represented by coordinates x and y, and the depth in the patient to be represented by z, the unscattered fluence,  at position
at position  with quadrature energy
with quadrature energy  was calculated as:
was calculated as:
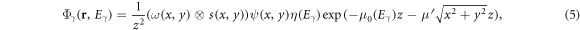
where  was a two-dimensional step function representing the beam aperture,
was a two-dimensional step function representing the beam aperture,  was the Gaussian source profile,
was the Gaussian source profile,  was the tabulated fluence profile of the radiation exiting the accelerator head,
was the tabulated fluence profile of the radiation exiting the accelerator head,  was the energy spectrum,
was the energy spectrum,  was the attenuation coefficient and
was the attenuation coefficient and  represented the off-axis softening of the beam. Note that ω and
represented the off-axis softening of the beam. Note that ω and  were actually functions of beam aperture size and shape, but that dependency is suppressed in the equation for simplicity.
were actually functions of beam aperture size and shape, but that dependency is suppressed in the equation for simplicity.
To assign the unscattered photon fluence to the quadrature orientations, the fluence calculated by equation (5) was assigned to the four orientation ordinates encompassing the beam orientation in a process analogous to bilinear interpolation. If the gantry angles of the ordinates were g1 and g2, the couch angles were c1 and c2, and the gantry and couch angles of the beam were g and c respectively, the fluence assigned to each of the four ordinates was given by:
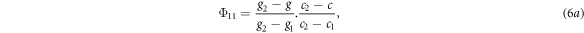
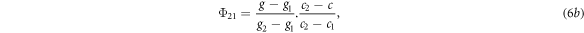
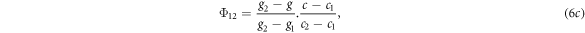
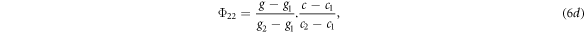
where the subscripts on Φ referred to the gantry and couch ordinates respectively.
The photon fluence was initially set equal to the unscattered fluence as calculated from equation (5) and (6). The dose calculation then solved the LBTEs for photons, to give the scattered fluence. Defining  to be a unit normal in the direction of interest, r to be the position of interest and
to be a unit normal in the direction of interest, r to be the position of interest and  to be the photon energy of interest:
to be the photon energy of interest:

where  was the electron density at position r,
was the electron density at position r,  was the scattered photon fluence at position r, with direction
was the scattered photon fluence at position r, with direction  and energy
and energy 
 was the differential Compton scattering cross section of a photon travelling initially with energy
was the differential Compton scattering cross section of a photon travelling initially with energy  in direction
in direction  and finally with energy
and finally with energy  and direction
and direction  and
and  was the total Compton scattering cross section (Hensel et al
2006). The integral term of equation (7) referred to scattered sources and was denoted as
was the total Compton scattering cross section (Hensel et al
2006). The integral term of equation (7) referred to scattered sources and was denoted as  where n indexed the discrete ordinates in the quadrature and i, j and k indexed the voxels in the patient model:
where n indexed the discrete ordinates in the quadrature and i, j and k indexed the voxels in the patient model:
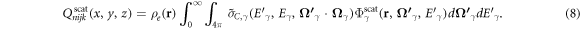
In practice, the integrals of equation (7) were discrete sums over the discrete ordinates. Moreover, a particle undergoing a scattering event for the particular angle between one direction of transport and another, with cosine  and ending with energy E, had a specific initial energy,
and ending with energy E, had a specific initial energy,  as governed by the kinematics of the scattering event. Consequently, the double integral collapsed to a single summation:
as governed by the kinematics of the scattering event. Consequently, the double integral collapsed to a single summation:
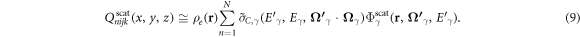
This required the initial interaction energy to be calculated for a given transition between the N angular ordinates and a given final energy. The equations given by Hensel et al (2006) were largely used for this purpose, leading to an N × N matrix of initial energies.
The differential and total scattering cross sections were also precalculated and stored at the beginning of each photon calculation. Again, the differential scattering cross sections were only needed for the specific angles between each of the ordinate directions, N × N items.
The differential cross sections for Compton scattering of both photons and electrons, together with the total cross section, were taken from Hensel et al (2006), based on Davisson and Evans (1952), and were straightforward to handle. Due to the coarse sampling of the angular quadrature, it was necessary to adjust the relative contributions of forward-scattered and large angle-scattered photons. Defining the cosine of the photon scattering angle to be θ, a threshold, θ0, was set. Then for  the differential scattering cross sections were weighted by a factor
the differential scattering cross sections were weighted by a factor  = 2.0, for
= 2.0, for  the differential scattering cross sections were weighted by a factor of
the differential scattering cross sections were weighted by a factor of  = 10.0 and the total scattering cross section was correspondingly multiplied by a factor of
= 10.0 and the total scattering cross section was correspondingly multiplied by a factor of  = 3.0. The value of θ0 was 1.0 in this instance, although lower values were also used in the validation (section 2.10). These factors were used for all types of tissue. The factors mostly affected the gradient and curvature of the depth dose curves, particularly in the region between 50 and 150 mm depth, where photon scatter formed a prominent part. They were chosen by varying them systematically to give good agreement of the calculated dose with measured depth-dose curves. Although this step was not physically exact, the empirical approach yielded satisfactory results.
= 3.0. The value of θ0 was 1.0 in this instance, although lower values were also used in the validation (section 2.10). These factors were used for all types of tissue. The factors mostly affected the gradient and curvature of the depth dose curves, particularly in the region between 50 and 150 mm depth, where photon scatter formed a prominent part. They were chosen by varying them systematically to give good agreement of the calculated dose with measured depth-dose curves. Although this step was not physically exact, the empirical approach yielded satisfactory results.
The equation (7) was solved using a series of transport sweeps (Lewis and Miller 1984). Within each iteration, a transport sweep was carried out for descending energy for each of the discrete ordinates. The sweep proceeded in either the x-, y- or z- direction, depending upon which octant the discrete ordinate direction was located in. If the voxels were indexed by i, j, k, bounded by x1/2, x3/2, ...xI+1/2, y1/2, y3/2, ...yJ+1/2, z1/2, z3/2, ...zK+1/2, with dimensions:
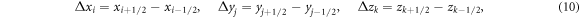
integrating the transport equation over voxels and dividing by  gave the relationship:
gave the relationship:
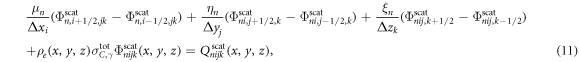
where μn , ηn and ξn were the direction cosines of the discrete ordinates, n (Hensel et al 2006). The following relationship was used to relate the fluence at the centre of the voxel to that at the edge:
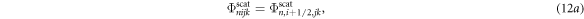

Comments (0)