The problem that we are interested in is the following: we assume that two residues, say A and B, in a protein interact, and this interaction is essential for allosteric activity. If the two residues are within the coordination shell of each other, they will interact through typical Lennard-Jones forces, including hydrogen bonds, electrostatic interactions, and steric effects. They may be spatially distant. In this case, the graph structure of the protein significantly influences their interaction [27, 28].
If a third residue C enhances the interaction between A and B, its effect is considered synergistic, forming what we term the allosteric channel. Conversely, C may provide overlapping information about the interaction between A and B that is already conveyed by either A or B. In information theory, this overlapping information is referred to as 'redundant'. However, in the context of proteins, C can be viewed as a backup residue that supports the A–B interaction, particularly if that interaction is weakened due to mutations or dynamic changes within the protein. Therefore, we will use the term 'redundant information' to mean 'overlapping information'. The residues that provide this information will be called 'redundant residues', but not in a negative sense.
Entropy of a residue A is represented by the Shannon equation [29]
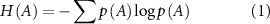
where, A represents the set of fluctuations of residue A, p(A) is the probability and H(A) quantifies the degree of uncertainty associated with those fluctuations. For correspondence between the thermodynamic entropy and the Shannon entropy, please see chapter 17 of the book by Callen [30].
Mutual information, 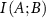 between A and B is defined as
between A and B is defined as
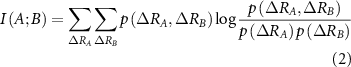
where, 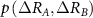 is the joint probability of fluctuations of residue A and B. The summation is carried out over all fluctuations of A and B. For brevity, the notation will be simplified by replacing
is the joint probability of fluctuations of residue A and B. The summation is carried out over all fluctuations of A and B. For brevity, the notation will be simplified by replacing 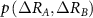 with
with 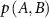 and
and  with
with 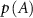 , etc, in the following.
, etc, in the following. 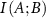 quantifies the reduction in uncertainty in the fluctuations of B that is achieved by knowing the fluctuations of A. If A and B are independent, meaning that knowing A gives no information about B, the mutual information is zero. However, if there is some relationship—whether linear or non-linear—mutual information will be positive.
quantifies the reduction in uncertainty in the fluctuations of B that is achieved by knowing the fluctuations of A. If A and B are independent, meaning that knowing A gives no information about B, the mutual information is zero. However, if there is some relationship—whether linear or non-linear—mutual information will be positive.
Joint entropy  is defined as,
is defined as,
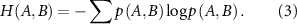
Conditional entropy 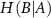 is defined as,
is defined as,
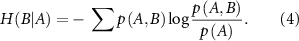
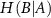 measures the amount of uncertainty remaining in the fluctuations of residue B when the fluctuations of residue A are known. It quantifies how much additional information is needed to describe B given that we already have information about A. When we observe the fluctuations of residue A, we may gain insights into the behavior of residue B. If knowing the state of A significantly reduces our uncertainty about B, then H(B∣A) will be low. This indicates that the fluctuations of A and B are correlated; when A fluctuates, B tends to fluctuate in a predictable manner.
measures the amount of uncertainty remaining in the fluctuations of residue B when the fluctuations of residue A are known. It quantifies how much additional information is needed to describe B given that we already have information about A. When we observe the fluctuations of residue A, we may gain insights into the behavior of residue B. If knowing the state of A significantly reduces our uncertainty about B, then H(B∣A) will be low. This indicates that the fluctuations of A and B are correlated; when A fluctuates, B tends to fluctuate in a predictable manner.
Mutual information is related to entropy by the equation
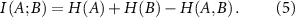
Conditional mutual information in terms of entropy is
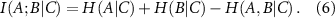
Conditional mutual information measures the amount of information that two random variables, A and B, share in the presence of a third variable, C. And finally, the interaction information
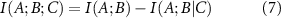
which represents a measure of how the information shared between variables A and B changes under the effect of another variable C. If the presence of C decreases the interaction between A and B, then 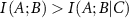 and
and 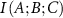 is positive. The amount of information provided by C to the interaction between A and B in this case has an overlapping component. The lowering of
is positive. The amount of information provided by C to the interaction between A and B in this case has an overlapping component. The lowering of 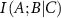 due to the presence of C may be due to two different effects that may be operating in the system. First, the presence of C may create mechanical noise, which may affect the direct correlation between A and B. Calculations show that the noise created by neighboring residues C along the primary chain increase the interaction information between A and B. The second effect occurs when C acts similarly to A or B in their interaction. In this case, C provides overlapping or duplicate information. This causes the conditional mutual information
due to the presence of C may be due to two different effects that may be operating in the system. First, the presence of C may create mechanical noise, which may affect the direct correlation between A and B. Calculations show that the noise created by neighboring residues C along the primary chain increase the interaction information between A and B. The second effect occurs when C acts similarly to A or B in their interaction. In this case, C provides overlapping or duplicate information. This causes the conditional mutual information 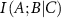 to decrease because C does not add unique information but rather repeats what A and B are already doing. This second case may indeed be useful for the protein to carry its allosteric function. It will be needed when the protein experiences mechanical stress, when one allosteric pathway is compromised, helps to ease-down negative effects of mutation, provides robustness against genetic variations, creates alternative information transmission routes, compensates for local structural fluctuations, maintains interaction integrity under perturbations, and prevents catastrophic information loss. The key point is that redundancy occurs when an additional element (C in this case) provides information that is already largely captured by the existing interaction between A and B. It is interesting to note that both redundancy and noise can lead to similar mathematical outcomes (positive interaction information), but they represent fundamentally different processes: redundancy strengthens or confirms existing relationships. Noise, on the other hand, introduces uncertainty and irrelevant information.
to decrease because C does not add unique information but rather repeats what A and B are already doing. This second case may indeed be useful for the protein to carry its allosteric function. It will be needed when the protein experiences mechanical stress, when one allosteric pathway is compromised, helps to ease-down negative effects of mutation, provides robustness against genetic variations, creates alternative information transmission routes, compensates for local structural fluctuations, maintains interaction integrity under perturbations, and prevents catastrophic information loss. The key point is that redundancy occurs when an additional element (C in this case) provides information that is already largely captured by the existing interaction between A and B. It is interesting to note that both redundancy and noise can lead to similar mathematical outcomes (positive interaction information), but they represent fundamentally different processes: redundancy strengthens or confirms existing relationships. Noise, on the other hand, introduces uncertainty and irrelevant information.
If the presence of C increases the interaction between A and B, which we call synergy, then 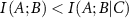 and the interaction information is
and the interaction information is 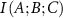 is negative. By identifying synergetic residues, it becomes possible to map potential allosteric paths. Such synergetic residues are essential in understanding long-range communication mechanisms.
is negative. By identifying synergetic residues, it becomes possible to map potential allosteric paths. Such synergetic residues are essential in understanding long-range communication mechanisms.
The interaction between A and B is subject to impulses from all other residues of the protein. The information received by A–B is 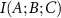 where C includes all residues other than A and B. The standard deviation (SD), of the information that comes to A–B is representative of the information transferred by C. Given this description of the signal I(A;B;C), the noise naturally comes from the SD of the conditional mutual information, SD(I(A;B|C)) showing the variability or uncertainty in the information transfer between A and B when accounting for all other residues. This SD quantifies the fluctuations and inconsistencies in how the other residues modulate the information exchange between A and B. Higher SD indicates more unpredictable or scattered information transfer, suggesting less stable or more complex interactions between A and B in the context of the entire protein. Thus, the signal to noise ratio,
where C includes all residues other than A and B. The standard deviation (SD), of the information that comes to A–B is representative of the information transferred by C. Given this description of the signal I(A;B;C), the noise naturally comes from the SD of the conditional mutual information, SD(I(A;B|C)) showing the variability or uncertainty in the information transfer between A and B when accounting for all other residues. This SD quantifies the fluctuations and inconsistencies in how the other residues modulate the information exchange between A and B. Higher SD indicates more unpredictable or scattered information transfer, suggesting less stable or more complex interactions between A and B in the context of the entire protein. Thus, the signal to noise ratio,  becomes
becomes
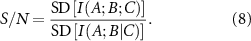
The signal-to-noise ratio (S/N) strongly depends on the spectral properties of the protein, particularly with larger eigenvalues of the Kirchhoff matrix being more representative of noise, while noise-like eigenvalues contribute more significantly to the denominator of equation (8).
Intramolecular noise provides insights into the robustness and adaptability of allosteric pathways, highlighting how internal redundancy or synergy can maintain effective communication despite perturbations. This perspective aligns with the principles of information theory, where variability in pathways can serve as a basis for error correction and signal reliability.
Finally, we consider the error correction capability of C. C provides overlapping information about the interaction between A and B, where transmission errors may occur. Here, we use the term 'transmission' in its broadest sense. For example, a sporadic impulse that tends to break a necessary hydrogen bond between A and B may be regarded as a transmission error that can be masked by the information sent by C. In this context, C acts as a molecular error correction code. Alternatively, if the A-B interaction is compromised or weakened, the overlapping information provided by residue C may reduce the uncertainty introduced. This suggests a natural error correction mechanism in protein communication pathways that compensates for imperfections in primary signal transmission and restores the integrity of the signals.
The GNM is a coarse-grained representation of proteins, where each Cα atom is modeled as a node in a graph, and edges connect nodes that are either covalently bonded or spatially proximate. The graph's connectivity is described by its Laplacian or Kirchoff matrix, Γ, which assigns unit entries to connected nodes and diagonal elements equal to the negative sum of each row. This Laplacian encodes the protein's local structural features, i.e. the residue interaction matrix, while its pseudoinverse is proportional to the fluctuation correlation matrix
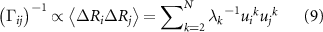
where, angular brackets denote average, i and j refer to residue indices, 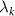 is the kth eigenvalue of β, and
is the kth eigenvalue of β, and 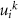 is the kth eigenvector of Γ for the ith residue. The model approximates fluctuations as isotropic, and despite this simplicity, it remarkably aligns with experimental observations of protein dynamics [7].
is the kth eigenvector of Γ for the ith residue. The model approximates fluctuations as isotropic, and despite this simplicity, it remarkably aligns with experimental observations of protein dynamics [7].
The GNM is based on the Laplacian matrix, which represents local interactions as linear springs, a characteristic feature of Gaussian distributions. A key strength of GNM lies in the inversion of the Laplacian matrix, which transforms local structural information into a global interaction map. In this transformed space, nonzero entries indicate indirect coupling, capturing generic correlations rather than strictly physical interactions between neighboring residues. In the original Laplacian, residue pairs that are physically distant are represented with zero entries due to the lack of direct interactions. However, the inverse Laplacian introduces nonzero entries for these pairs, capturing the indirect interactions mediated through the network, which automatically contributes to the mutual information between distant residue pairs. These nonzero values reflect dynamic couplings between residues, offering insight into long-range relationships within the protein. This capability to account for allosteric interactions in a single computational step distinguishes GNM from other methods.
In addition to providing structural insights, GNM captures protein dynamics by analyzing the eigenmodes of motion derived from the Laplacian [8]. These eigenmodes explain collective movements and pathways that underlie functional processes such as allosteric signaling. The Laplacian has a zero eigenvalue, which corresponds to rigid body motion. Smaller eigenvalues characterize slow and large scale motions and larger eigenvalues correspond to fast motions that are more noise-like. By integrating both structural and dynamic information, GNM offers a computationally efficient framework for studying information transfer and long-range communication within proteins, making it the simplest yet powerful approach for such analyses.
Entropy for n variables for a multivariate Gaussian distribution of fluctuations reads as
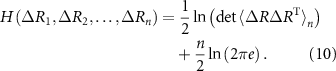
Expressions for mutual information, conditional mutual information and interaction information are obtained from the entropy using equations (3)–(7).
Substituting from equation (10), which works for a Gaussian system, leads to the following [31]
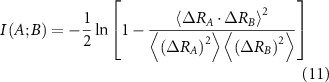
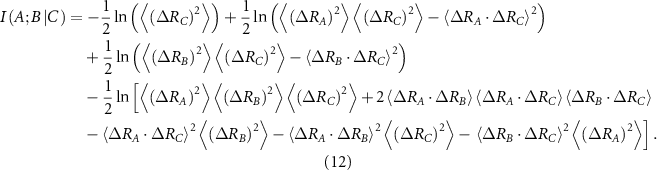
The derivation of equations (11) and (12) are explained in [18] and the supplementary information section of that reference. All entries in equations (11) and (12) follow from the inverse of the Laplacian and their use in the interaction information expression, equation (9). Scanning over the protein by keeping A and B fixed and changing C leads to the interaction information profile for the protein in which positive peaks show the backup residues that provide overlapping information and negative peaks show the synergistic residues for the interaction between residues A and B.
When C equals A or B, then the right hand side of equation (7) is undefined, but since  we have
we have
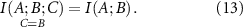
Comments (0)