Low latency computing for time stretch instruments

State-of-the-art deep neural networks with billions of parameters have been deployed for various applications including computer vision, speech processing, engineering design, and scientific discovery. The ever-increasing complexity of the networks is powered by the advances in semiconductor technology described by the Moore's law. The projected end of the Moore's law is a concern for the future evolution of neural networks [1]. Additionally, the neural networks must be trained and this requires a massive amount of labeled data the number of which scales with the network complexity. The unavailability of curated data in many domains precludes the use of deep neural networks. The inference speed of the current neural networks is typically in the millisecond timescale. This is at odds with ultrafast optical sensors which can acquire data at femtosecond time intervals and at picosecond frame intervals.

This calls for a new look into the approaches that can work in ultrafast timescales with a limited amount of data. Analog computing [2] is a promising approach that performs specialized computing in complex nonlinear systems to take over the burden from the digital computer. Photonic hardware accelerator is such an approach that focuses on instantiating complex mathematical models in optical systems. For example, a convolutional neural network can be emulated by a stack of spatial light modulators [3]. A feed-forward neural network can be implemented on a photonic chip using an interconnected photonic circuit [4]. A photonic reservoir computer can be assembled using an optical amplifier along with a feedback loop [5]. However, all demonstrated works are either complex in structure or need a significant increase in data dimensionality, which has held back their practical application.

Recently, a technique for performing data classification in the ultrafast timescale, called Nonlinear Schrödinger Kernel has been introduced [6]. It draws an analogy to numerical kernel computing which employs a nonlinear transformation of data without explicitly increasing the data dimensionality. It utilizes optical nonlinearities to map the data onto a new domain in which classification accuracy is enhanced. This is done by modulating the data onto the optical spectrum of a femtosecond pulse and performing complex nonlinear transformation through a nonlinear optical media. Therefore, it was originally developed for applications such as time stretch instruments where in the measurement process, data is encoded onto the spectrum of an ultra short laser pulse. Previous studies have shown that this technique achieves similar results as a traditional numerical kernel with orders of magnitude lower latency on small datasets. Moreover, it does not increase the dimension of data and hence does not sacrifice the computing resource. One of the limitations of this technique has been the fixed optical transfer function, which prevents training and generalizability, meaning the performance is highly dependent on the dataset.

To solve this problem, we propose an approach to tune and optimize the nonlinear optical transfer function of the kernel. While the nonlinear optical system parameters cannot be tuned, the nonlinear process can be effectively engineered by varying the phase of the input data [7]. This is based on the insight that most nonlinear interactions, such as self-phase modulation, four-wave mixing, etc are coherent processes that depend on the input phase. Therefore, tuning the spectral phase of the input data will inevitably change the nonlinear interaction among spectral components. Since the data is encoded onto the spectrum, this process changes the nonlinear interaction among data dimensions.

In this paper, we first investigate the key effect inside the optical kernel and then propose a tuning scheme utilizing complex data encoding. To evaluate the effect of tuning, a digital feedback loop is added to the system to obtain the optimal phase code that gives the best classification accuracy. The effect of phase encoding and optimization is demonstrated on three datasets: time stretch cell image [8], phalanges bones outline [9], and electroencephalogram (EEG) [10].

Figure 1 shows the system block diagram featuring closed-loop optimization of the optical kernel. This system contains a highly tunable Nonlinear Schrödinger Kernel, and a digital feedback loop. In the tunable kernel, the input $}\left( n \right)$ is mapped into the spectrum domain ($}\left( \omega \right)$) and amplitude modulated onto a supercontinuum laser pulse. The data then travels through a nonlinear optical element where it is nonlinearly transformed. The transformed data is finally captured by a spectrometer and sent to a backend digital classifier which adopts a light machine learning model. To avoid increasing data dimensions, the output spectrum of the kernel is sampled to match the dimension of the input data. The tuning is achieved by modulating a spectral phase $\phi \left( \omega \right)$ onto the laser pulse during spectral modulation, equivalent to encoding the phase of the input data. This 'phase code' modifies the nonlinear interaction in the nonlinear element and hence engineers the optical kernel. In the digital feedback loop, the algorithm compares the predictions with the ground truth and calculates the average classification error for the whole dataset. Subsequently, a new phase code is generated by an optimizer who aims at minimizing this error. The system runs iteratively to obtain the optimal phase code, through which the optical kernel is trained for optimal performance. The details of the experiment system can be found in the Methods section.

Figure 1. Optimization of a tunable Nonlinear Schrödinger Kernel. The system contains a tunable Nonlinear Schrödinger Kernel and a digital feedback loop. In the tunable Nonlinear Schrödinger Kernel, the phase-encoded input $}\left( n \right)$ is mapped onto the spectrum of a supercontinuum laser via spectral modulation. The modulated laser propagates through a nonlinear optical element, where the nonlinear process is engineered by the phase code $\phi \left( \omega \right)$. The output spectrum of the nonlinear optical element $}}}$ is then acquired using a spectrometer and sent to a classifier $F$. The classification error is calculated by comparing the predicted class $}}}$ and the ground truth $}}}$. This error is used as an input to an optimization algorithm to update the phase code for achieving lower classification errors. The details can be found in the Methods section.

Download figure:

Standard image High-resolution image

This system achieves optimization of the kernel by engineering the optical nonlinearity through spectral phase encoding. It is based on the fact that the optical nonlinearity is coherent and therefore sensitive to the optical phase, and the optical nonlinearity plays a critical role in the Nonlinear Schrödinger. To demonstrate its significance, we isolate the nonlinear effect since achieving this in a physical system is unfeasible, we rely on simulations based on the mathematical model of the Nonlinear Schrödinger Kernel. Subsequently, we perform actual physical experiments using the implemented system to further validate this technique. This study involves three datasets. Three datasets are involved in this study. To demonstrate the compatibility of this technique with time-stretch technology, we introduce the time stretch microscope cell image dataset, which was collected using a time stretch instrument [8]. In addition, we utilize two open-source datasets: the phalanges bones outline [9] and EEG [10]. These datasets are employed to showcase the broad range of potential applications for this technique.

The details of the study are provided in the Methods section (section 6). The physical implementation of the system is described in section 6.1. The MATLAB simulation is explained in section 6.2. The derivation of the mathematical model is presented in section 6.3. Finally, section 6.4 introduces the datasets used in this study.

The main subject of this paper is the optimization and training of the nonlinear optical kernel. We first describe the critical importance of nonlinearities in this approach.

3.1. The crucial role of optical nonlinearity

In figure 2 we show via simulation the evolution of a femtosecond pulse, that has been spectrally modulated with data, through the nonlinear optical element. The output spectrum is classified using a simple machine learning algorithm. Also shown in figure 2 is the error produced by using a linear support vector machine (SVM) classifier as the digital backend. Here the nonlinear kernel is fixed, i.e. not tuned. As described in the Methods section, the data is the 1-D linescan images of biological cells flowing through a microfluidic channel. The images are captured by a time stretch microscope [8, 11]. The dataset contains three types of images: (1) no cell is present, (2) a normal cell, and (3) a cancer cell. The classification task is to distinguish between three different types.

Figure 2. (a) The evolution of the optical spectrum in the linear optical kernel where nonlinear coefficient $\gamma = 0\;} \cdot }} \right)^}$(b) The evolution of the optical spectrum in the nonlinear optical kernel where $\gamma = 11\;} \cdot }} \right)^}$. (c) Bar chart comparing the classification error for three cases: the baseline error calculated without kernel (blue, 14.7%), the linear optical kernel (green, 14.9%), and the nonlinear optical kernel (orange, 7.8%). The baseline error is calculated by directly feeding the input data to the digital backend, which in this case is a linear support vector machine (SVM) classifier. For (a) and (b), the x axis is the wavelength, the y axis is the propagation distance (normalized to the effective length of the optical element). The color indicates the optical intensity in the log scale with color bar on the side. The red arrow point to the propagation direction.

Download figure:

Standard image High-resolution image

In figures 2(a), a linear kernel is simulated by setting the nonlinear coefficient to zero. As expected, the optical spectrum remains unchanged. As shown in figure 2(c) the classification error remains almost unchanged at 14.9% compared to the 14.7% baseline error obtained by feeding the data directly into the backend digital classifier. Figure 2(b) shows the propagation of the same spectrally modulated pulse in the nonlinear element. To avoid an increase in data dimension, we operate in the spectrum narrowing regime. This occurs when the pulse undergoing self-phase modulation has a negative chirp [12]. The output spectrum is sampled such that it has the same dimensions as the input data (128) as explained in the Methods section. The nonlinear transformation reduces the classification error to 7.8%, confirming the utility of the optical kernel in enhancing machine learning without sacrificing (i.e. increasing) the data dimensionality.

Comparing the effect of linear and nonlinear kernels in figure 2, it can be observed that the enhancement in classification accuracy cannot be achieved without optical nonlinearity. However, as a proper machine learning technique, the nonlinearity must be tunable so it can be optimized. Previous research has demonstrated the successful control of optical nonlinearity using the spectral phase modulation of the input light. Here we apply to same technique to tuning and optimization of the nonlinear optical kernel where the optimization is guided by the classification error (figure 1).

3.2. Training of optical nonlinearities for machine learning

In this section, we demonstrate that the nonlinear optical kernel can be tuned by applying phase encoding to the input data. As mentioned in the introduction, the intuition behind this approach is as follows. Nonlinear optical interactions such as self-phase modulation, four wave mixing, etc are coherent in nature, i.e. they are affected by the phase of the input pulse. It then follows that manipulating the input phase influences the output produced by the optical nonlinearity.

The experimental implementation is shown in figure 1. Spectral phase modulation within a digital feedback loop controls the nonlinear optical interactions and hence tunes the optical kernel. A genetic algorithm arrives at the optimal phase code that minimizes the error of the digital classifier. The results for three datasets are experimentally demonstrated. The datasets described in the Methods section include cell images (figure 3(a)), phalanges bones outline (figure 3(b)), and EEG (figure 3(c)).

Figure 3. Optimization of Nonlinear Schrödinger Kernel on three datasets: (a) time stretch biological cell image (b) phalanges bones outline (c) electroencephalogram (EEG). In each bar chart, the classification error for three cases is compared: baseline error (gray), untrained Nonlinear Schrödinger Kernel (blue), and trained Nonlinear Schrödinger Kernel (orange). The baseline error is calculated by feeding the input data directly into the digital backend—a linear support vector machine (SVM) classifier. All the results are calculated via 3-fold cross validation.

Download figure:

Standard image High-resolution image

Figure 3 shows that, in all three datasets, both the trained (orange), as well as the fixed (untrained) kernel (blue), produce a lower error rate compared to the baseline case where no optical kernel is used (gray). However, the trained optical kernel leads to a lower error than the fixed kernel. The baseline error is obtained by feeding the input data directly to the digital backend. The results prove that the phase encoding can effectively tune the performance of the Nonlinear Schrödinger Kernel, and combined with the digital feedback loop renders the optical kernel trainable.

In these experiments, the phase code is generated using a polynomial with two tunable parameters for the second-order and the third-order coefficients. This scheme can be easily expanded to more parameters to provide additional degrees of freedom. Details of the experiments are also in the Methods section.

Some of the limitations of this technique and potential future research are as follows. First, the maximum allowed dimension of the input data is dependent on spectral modulation. In our experiments, we use a commercial waveshaper (details in the Methods section) with 500 pixels. This limits the maximum dimension of the input data to 500. Second, even though the kernel can be trained, the performance in terms of classification error is still data-dependent, as seen in figure 3. Such is the case with all machine learning techniques because they are statistical in nature (as opposed to deterministic). One possible direction for future research is to correlate the classification performance with the properties of the input data to identify the type of data for which optical kernel computing is most effective.

The recently introduced optical kernel computing utilizes optical nonlinearities to transform data such that nonlinear classification can be done with a computationally light linear digital classifier. The so-called Nonlinear Schrodinger Kernel computing is ideal for low latency classification of data that is modulated onto the spectrum of femtosecond lasers. Such is the case with time stretch imaging and spectroscopy instruments [13, 14]. In the previous implementation of this technique, the property of the kernel was entirely governed by the nonlinear coefficient of the optical medium. Hence the kernel could not be trained or optimized as required in machine learning tasks. In this paper, we presented a solution to this predicament by introducing spectral phase modulation of the input pulse within a digital feedback loop. Phase modulation influences how data is transformed by nonlinear optical interactions and allows the optical kernel to be trained. The training is shown to reduce the classification error on three diverse datasets.

In this section, we provide details of (1) experimental implementation for kernel optimization, (2) simulation study showing the critical role of optical nonlinearities, (3) mathematical formulation of the optical kernel, and (4) the datasets and machine learning model.

6.1. Experiments

The physical implementation of the closed loop optical kernel computing system follows figure 1. The supercontinuum laser is a mode-locked Erbium-doped fiber laser followed by an Erbium-doped fiber amplifier, both from Menlo Systems. It produces $ < }90}$ laser pulses centered at $1560}$ with $90}$ bandwidth. The approximate pulse peak power is $30}$ after the amplifier. The data modulates the optical spectrum using a Finisar (now II–VI/Coherent) Waveshaper model 1000 S L−1. It operates in the L band ($1567}\sim}1609}$) with a 500-pixel resolution. The Waveshaper performs both amplitude and phase modulation simultaneousl. The amplitude is the input data (scaled between 0 to 1), while the phase is the (phase) code that is applied to tune the nonlinear effects. The nonlinear optical element is a 500 m highly nonlinear fiber (HNLF) from Corning. It has a nonlinear coefficient $\gamma = 11\;} \cdot }} \right)^}$, a low dispersion of $D = 1.43}\,} \cdot }} \right)^}$, and dispersion slope $S = 0.04}\,}}^2} \cdot }} \right)^} - }}}$at $1588}$. An Ando AQ6317B optical spectrum analyzer with $0.1}$ resolution measures the output spectrum. The sampling range of the spectrum analyzer is set differently for each dataset depending on the actual bandwidth of the output. For the cell image and phalanges bones outline dataset, it is 1545 nm–1635 nm. For the EEG dataset, it is 1550 nm–1630 nm. The measured spectrum is resampled so that it has the same dimension as the input. It is then min-max standardized and sent to a linear SVM classifier.

The digital feedback loop is implemented in MATLAB on a computer with 16 GB RAM memory. It runs iteratively to optimize the performance of the Nonlinear Schrödinger Kernel. In each iteration, the classification error rate is the average over the entire dataset and is calculated via three-fold cross validation. It is sent to the optimizer which is a genetic algorithm from MATLAB Global Optimization Toolbox [15]. To minimize the classification error, it compares the result from the current iteration with the previous ones and generates the phase code for the next iteration. In this paper, the phase code is by a third-order polynomial with adjustable coefficients,

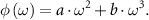
Here, a and b are the tunable coefficients generated by the optimizer. The first-order coefficient is not taken into consideration as it simply causes a constant delay and does not affect the nonlinear optical process. The optimization results are shown in figure 3. The optimal coefficients for the cell image dataset (figure 3(a)) are shown in table 1. The optimized classification error, $Er}}}$ are also attached in comparison with the unoptimized classification error $Er}}}$ and the baseline error $Er}}}$.

Table 1. Optimal phase code.

 Cell ImagePhalanges Bones OutlineElectroencephalogram (EEG) a(×10−24)1.3530.8541.022 b(×10−37)−3.6280.925−4.742 $Er}}}$ 4.5%27.5%30.7% $Er}}}$ 8.0%31.5%36.04% $Er}}}$ 15.0%35.2%30.7%6.2. Simulation

To assess the role of optical nonlinearities in the operation of the Nonlinear Schrödinger Kernel, a computer model is created in MATLAB. The supercontinuum laser source is modeled as a transform-limited pulse with a supper-Gaussian spectrum centered at $1588}$. It has a $40}$ bandwidth consistent with the passband of the spectral modulator (waveshaper). The spectral modulation is modeled by multiplying the input data (time stretch cell image data, scaled between 0 to 1) by the laser spectrum. For these simulations, the phase code is set to 0 to simulate the unoptimized (open loop) system. The modulated laser pulse is then sent through a nonlinear optical element, in this case, an HNLF. The complex propagation in the fiber is modeled by solving the time domain Nonlinear Schrödinger Equation (NLSE) using the split-step Fourier method (SSFM) implemented in MATLAB. This algorithm divides the fiber into short segments (steps). In each step, the time demon optical nonlinearity and spectral domain dispersion can be separated. For example, the nonlinearity only exist for the first half of the step, and the dispersion only exist for the other half. Since the analytical solution exist for both situation, the numerical solution for one step can be obtained. Computing step-by-step, we can obtain an approximate solution [12]. In each step, the spectrum of the optical pulse is recorded to track the evolution of the input, as shown in figure 2. The output of the HNLF is measured using a spectrometer, which is modeled by a fast Fourier transform and absolute square. Finally, the collected spectrum is resampled so that it has the same dimension as the input, mean-std standardized, and sent to a linear SVM classifier.

For the simulation shown in figure 2, the length of the fiber is set to $500}$. The optical loss is $0.02}\,}}^}$, the dispersion coefficient ($D$) is $1.43}\,} \cdot }} \right)^}$, the dispersion slope ($S$) is $0.04}\,}}^2} \cdot }} \right)^}$ at $1588}$, and the optical power $P$ is

View original article
JOURNAL OF PHYSICS-PHOTONICS

Comments (0)

No login
gif
format_indent_decrease