Functional electrical stimulation (FES) for artificial generation and support of movements through application of electrical currents represents a promising tool in the rehabilitation of certain neurological patients. Rehabilitation, at its root, has the purpose of forming new neural connections in lieu of damaged ones, typically between the central and the peripheral nervous system, by re-training the patient to perform movements or tasks. FES offers many advantages with respect to rehabilitation facilitated through externally exerted forces, mainly because the patient's muscles are stimulated and thus actively employed for task completion, thus avoiding secondary complications such as muscle atrophy. In the early phase of rehabilitation, FES can be used as an effective tool in a task-specific, restorative therapy program to foster neurological recovery [1]. In the chronic phase after a neurological disease or trauma, FES may still be used as a neuroprosthesis for compensation of completely lost or very weak motor functions. Particularly in individuals with spinal cord injury (SCI) and the associated functional impairments, FES has been successfully employed for assistance in activities of daily living (ADL), both using trans-cutaneous [2] and intramuscular electrodes [3]. Non-invasive FES applied through surface electrodes is also used in applications outside of the medical field, for example VR and AR [4].
Most control schemes focus on restoring functional, task relevant movements, such as reaching and grasping [2, 3], and focus on the identification of the dynamics relevant to these [5, 6]. Such parameters, however, are not guaranteed to generalize well over different postures. On the one hand, black box approaches typically have to sample the effects of muscle contractions in various postures [7, 8]. Musculoskeletal models, on the other hand, can inherently account for at least some effects of posture changes[9, 10]. In robotics, impedance-based controls can be used to impose a certain dynamic behaviour between a robot and its environment [11]. Impedance controls are robust in terms of kinematic singularities, and can be well integrated in wider motion-planning algorithms, but the main purpose of impedance control is to facilitate the interaction of a robot with an unpredictable environment with non-linear dynamics [11]. However, the characteristics of impedance control make it robust also with respect to actuators exhibiting these characteristics, as can be human muscles. A suitable impedance could facilitate conversion from a positional error into a desired force output, which is more directly correlated to muscular activity. FES-based force controls have been proposed, among others, in [7, 12, 13]. These works all present black box models of the endpoint force output as a consequence of FES. In the context of FES, a suitable impedance control could be used to assist movements towards any desired point in the user's peri-personal space, leading to a more general-purpose paradigm, which could be beneficial in rehabilitation, but especially in the case of FES used as a neuroprosthesis. Razavian et al present a demonstration of such a concept [7]. The compliant nature of the human body could allow for the safe inclusion of the positional error's integral over time in the impedance, which would lead to increased robustness with respect to modelling errors. Integrative terms are often excluded from impedance controls in conventional robotics, as they would cause an increase of force output over time, should the robot encounter an obstacle preventing it from reaching the desired pose. In such a scenario, the robot could cause damage to itself or its surroundings if its force output is not limited.
This paper should serve as a system description of the FES device, which consists of a wearable surface stimulation device designed to provide proportional force control through FES on the upper limb of a user on up to 10 channels with a resolution of 16 bits, and assess its capability to induce a desired force output in real time. Because of its practicality and versatility, surface FES is widely used in commercially available products, such as the Teslasuit® platform (VR Electronics Ltd., London, UK). This device has been successfully employed in user studies with able-bodied participants [14], and represents a good commercial benchmark, as it integrates various sensor modalities and gel-less surface stimulation electrodes. However, this system cannot adjust well to different body frames, and the electrode arrangement cannot be modified. The device proposed here, on the other hand, features a Velcro-lined compressive jacket which allows for easy modifications in electrode arrangement to fit any user frame. The jacket also increases repeatability of electrode placement once the ideal arrangement for an individual user has been established.
While this device proposes to be a general-purpose platform designed to test various control algorithms, here the system is driven by a musculoskeletal model presented and validated in [9]. Therein, the musculoskeletal model was tested against a third-party model introduced in [10], which was taken as baseline. The model associates a line of action to each stimulated muscle group, as exemplified in [15]. A core principle and fundamental goal in the design philosophy of this system is the adaptability to different users. In order to achieve this, the musculoskeletal model can be easily modified to better fit each individual without the need for much anatomical expertise. To this end, a calibration procedure able to adjust the model geometry is also introduced here. Canonically, a model based on line of action relies on a line running through the average centroid of the physiological cross section along the whole length of the stimulated muscle groups, as introduced in [16] and, more recently, in [17]. Many studies have demonstrated how inhomogeneities in muscle activation can lead to great effects on joint momenta. In the case of the musculoskeletal model used here, the reconstruction of the line of action is based on the observation of functional effects of muscle contraction on the musculoskeletal system in a given position, as introduced among others in [18]. Here, the model uses a fast and computationally efficient Nearest Neighbour recruitment strategy to calculate the stimulation currents necessary to cause a given endpoint force output.
The system is validated in an online experiment where the FES-induced force output of 3 able-bodied volunteers is compared to a desired force output. Part of these results were published in [19]. In addition, we evaluate the performance of an offline-trained predictor which is able to precisely predict the force output both in task space and in joint space based on the stimulation currents. Such a predictor could be trained based on data from a force-torque sensor prior to the normal operation of the device in a setup similar to the one used during the online system validation.
2.1. Musculoskeletal modelThe line of action associated to every stimulated muscle group is routed through a series of points lying on a curve between an origin  and an insertion point
and an insertion point  . In general, we can consider the line of action as a continuous curve in 3D space, with all intermediate positions
. In general, we can consider the line of action as a continuous curve in 3D space, with all intermediate positions  between
between  and
and  defined by a scalar parameter
defined by a scalar parameter ![$l\in [_,_]\subset }$](https://content.cld.iop.org/journals/2057-1976/9/6/065008/revision2/bpexacf04bieqn6.gif?Expires=1695249804&Signature=rgEKMMYN-W-vzZqtmLxMCj1VLaHVdE1NAJZqjzbErluBMPDmDjbLwlbX8CS4QgyiqKfshppvaQ-nn2Q7dmNEapghplYk41v3gvRg0ZTosT0JuSgRkjcP2AhocHU9R7IRmF2YzpyK9NjJjlOU9qaiFjmTbKhWvxxCyuBvaMfCJV5F5iT59528VQTYUfT5JKZmppucdaZ8XUFtqIv52OnVc~wDQEyvZ6ZJ~NXp8X875Awi~58N6bvTmo4GtUmlWq9Z8cSx6R1iSRUHFwtqzo-0abfObj-hEEmRaJAO6CfLLAHoLk4LfH59IQuviE81rrZ3Ksk7VneI3LmVA0~jM11cFA__&Key-Pair-Id=KL1D8TIY3N7T8) , so that
, so that  and
and  , as shown in figure 1(a).
, as shown in figure 1(a).
Figure 1. (a): Conceptual depiction of the process by which a muscle can be modeled as a continuous curve an then lumped into a single prismatic actuator able to exert a force by contracting along the direction of the vector  , and having an effective lever arm
, and having an effective lever arm  , thus enabling the actuator to apply a torque
, thus enabling the actuator to apply a torque  about the joint
about the joint  . Every joint is modelled as having 3 revolute axes. (b): The musculoskeletal model. Each electrode pair is associated with a red line. The labels represent the channel numbers. The joints are also labeled.
. Every joint is modelled as having 3 revolute axes. (b): The musculoskeletal model. Each electrode pair is associated with a red line. The labels represent the channel numbers. The joints are also labeled.
Download figure:
Standard image High-resolution imageThe muscle groups stimulated by one electrode pair are considered as a string routed along the line of action's curve, with the muscle force being exerted homogeneously in a tangential direction, which is to say that the force along the line of action has constant module  . Given this, knowing the line of action's routing in 3-D space, we can compute the average force vector
. Given this, knowing the line of action's routing in 3-D space, we can compute the average force vector  through
through
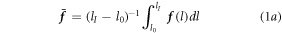
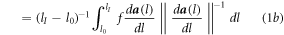
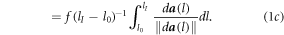
Following the same rationale, we can calculate an average torque vector  exerted by the muscle group about the joint's position
exerted by the muscle group about the joint's position 
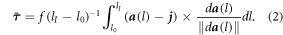
Reducing the points on the curve to a finite set of  points
points  , equation (2) becomes a sum of the form
, equation (2) becomes a sum of the form
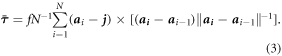
The average force  and average torque
and average torque  derived from the line of action characterize a lumped model of the muscle, which behaves like a prismatic joint able to exert a force f determined by the stimulation in the direction
derived from the line of action characterize a lumped model of the muscle, which behaves like a prismatic joint able to exert a force f determined by the stimulation in the direction  by contraction, with an average effective moment arm
by contraction, with an average effective moment arm  , which results in a torque
, which results in a torque  about the joint at position
about the joint at position
 with revolute axes
with revolute axes  , as depicted in figure 1(a). Depending on which skeletal segments the muscle group originates from and inserts into, this prismatic actuator approximation of the stimulated muscle group can exert a torque around more than one of the skeleton's rotational axes. In particular, if the
, as depicted in figure 1(a). Depending on which skeletal segments the muscle group originates from and inserts into, this prismatic actuator approximation of the stimulated muscle group can exert a torque around more than one of the skeleton's rotational axes. In particular, if the  -th degree of freedom is a revolute joint at position
-th degree of freedom is a revolute joint at position  with its axis pointing in a known direction
with its axis pointing in a known direction  , if a muscle group is able to exert a torque about it, we can reduce the expected torque computed as shown in equations (2) and (3) to a scalar torque magnitude
, if a muscle group is able to exert a torque about it, we can reduce the expected torque computed as shown in equations (2) and (3) to a scalar torque magnitude  by computing
by computing
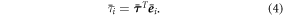
If the muscle group is not able to exert a torque about the  -th degree of freedom, on the other hand, the scalar projection of the expected torque onto joint space is 0. As depicted in figure 1(a), every joint in the musculoskeletal model is modelled as having 3 revolute axes. This is done due to the difficulty of reliably measuring the direction of the anatomically correct revolute axes. This makes every joint in the model as depicted in figure 1(b) defined by a single position
-th degree of freedom, on the other hand, the scalar projection of the expected torque onto joint space is 0. As depicted in figure 1(a), every joint in the musculoskeletal model is modelled as having 3 revolute axes. This is done due to the difficulty of reliably measuring the direction of the anatomically correct revolute axes. This makes every joint in the model as depicted in figure 1(b) defined by a single position  and 3 revolute axes.
and 3 revolute axes.
The line of action's routing can be initially set based on cursory anatomical expertise and the known electrode placement, but can be further adjusted based on the measured response to stimulation pulses. Here, a simplified calibration procedure is implemented. This is based on the assumption that the average force vector  should lie in the plane in which the limb moves when a stimulation pulse is applied. The calibration finds the points
should lie in the plane in which the limb moves when a stimulation pulse is applied. The calibration finds the points  for each line of action which minimize the difference between the expected and the measured torque output in joint space resulting from the stimulation pulse. Although this condition could be satisfied even if the line of action were not to lie entirely on this same plane, this is assumed for simplicity's sake. A stimulation pulse causes an average torque
for each line of action which minimize the difference between the expected and the measured torque output in joint space resulting from the stimulation pulse. Although this condition could be satisfied even if the line of action were not to lie entirely on this same plane, this is assumed for simplicity's sake. A stimulation pulse causes an average torque  over the pulse time, which in turn causes the body segments distal to the affected joint at position
over the pulse time, which in turn causes the body segments distal to the affected joint at position  to accelerate at an angular acceleration rate
to accelerate at an angular acceleration rate  , where
, where  is the cumulative moment of inertia of the distal body segments, which is assumed to be constant throughout the stimulation, and
is the cumulative moment of inertia of the distal body segments, which is assumed to be constant throughout the stimulation, and  is the angular acceleration vector due to the twitch. In this study, the moment of inertia was calculated based on the user's mass and the anthropometric tables from [20]. Over the course of this study, the participants were directed to hold their arm in the starting position voluntarily, and therefore the influence of gravity was assumed to be compensated by volitional muscle contraction. Assuming, furthermore, a constant acceleration rate during the stimulation pulse, and an initial rest state of the joint, the distal body segments reach a maximum angular velocity
is the angular acceleration vector due to the twitch. In this study, the moment of inertia was calculated based on the user's mass and the anthropometric tables from [20]. Over the course of this study, the participants were directed to hold their arm in the starting position voluntarily, and therefore the influence of gravity was assumed to be compensated by volitional muscle contraction. Assuming, furthermore, a constant acceleration rate during the stimulation pulse, and an initial rest state of the joint, the distal body segments reach a maximum angular velocity  , where
, where  and
and  are the times at which the stimulation starts and ends, respectively. Therefore, we have an approximate proportionality between the maximal observed angular velocity and the expected torque of the stimulated muscle group, namely
are the times at which the stimulation starts and ends, respectively. Therefore, we have an approximate proportionality between the maximal observed angular velocity and the expected torque of the stimulated muscle group, namely
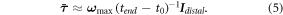
The plane of movement for the limb is defined as passing through the joint's position  and being normal to the angular velocity vector
and being normal to the angular velocity vector  of the twitch itself. As shown in figure 2, based on the observed twitch
of the twitch itself. As shown in figure 2, based on the observed twitch  , the position of the origin point
, the position of the origin point  and the insertion point
and the insertion point  are set over the
are set over the  and
and  coordinates, respectively, in order to minimize the distance of the two points from the twitch plane passing through
j
and normal to
coordinates, respectively, in order to minimize the distance of the two points from the twitch plane passing through
j
and normal to  . Here,
. Here,
 and
and  are the azimuth of the origin and insertion point, respectively, expressed in a cylindrical coordinate frame the height axis of which corresponds to the longitudinal axis of the proximal body segment in the case of the origin point and the distal body segment for the insertion point, as shown in figure 2. The origin and insertion point positions are additionally defined by a radius
are the azimuth of the origin and insertion point, respectively, expressed in a cylindrical coordinate frame the height axis of which corresponds to the longitudinal axis of the proximal body segment in the case of the origin point and the distal body segment for the insertion point, as shown in figure 2. The origin and insertion point positions are additionally defined by a radius  and
and  , respectively, and a height
, respectively, and a height  and
and
Comments (0)