XUV plasmonic waveguides by near-zero index heterostructures

The lack of transmissive photonic components in the extreme ultraviolet (XUV) constitutes a challenge for micro/nano-metric confinement. Here, we theoretically design a novel approach to attain XUV radiation guidance based on the electromagnetic properties of titanium–aluminum–titanium heterostructures in such a spectral domain. We show that, thanks to the near-zero-index properties of aluminum and titanium, XUV radiation can couple efficiently with plasma oscillations in such heterostructures, enabling the excitation of several distinct plasmon polariton modes. Our predictions, based on the semi-analytical solution of fully vectorial Maxwell's equations, indicate that the dispersion profile of plasmon polariton modes can get efficiently modulated by the aluminum thickness, enabling nanometer confinement and micrometre propagation length. Moreover, we quantify the third-order nonlinearity enhancement factor, finding that it is resonant at the zero-index wavelength. Our results are promising for the development of future devices enabling advanced control and manipulation of XUV radiation.

Extreme ultraviolet (XUV) radiation provides two main advantages with respect to optical radiation: (i) a shorter wavelength, enabling a more efficient lithography [1] and a more efficient pulse compression of few-cycle pulses to achieve attosecond time-scale [2–6] and (ii) a selective probing of specific core electrons, enabling spectroscopy with atomic selectivity [7, 8]. These properties, with the advent of pulsed sources based on high-harmonic generation and free-electron lasers have stimulated a large interest in physics and chemistry, providing theoretical insight of new spectroscopic schemes [9–13], and recent experimental implementations, e.g. nonlinear spectroscopy [14], coherent multidimensional spectroscopy [15, 16], soft x-ray photo-ionization [17], time-resolved XUV transient absorption [18–21], and time-resolved chiral order detection [22]. Such emerging ultrafast techniques enable the probing of molecules and materials in condensed phase by photons with high energies in the XUV and are opening novel avenues to our basic understanding of ultrafast relaxation, non-equilibrium processes and chemical reactions [23]. Moreover, nonlinear interaction of matter with XUV radiation enables advanced photonic applications, e.g. wave-mixing [24, 25], second-harmonic generation [26, 27], saturation of absorption [28] and self-induced spectral tuning [29]. However, the inherently weak light–matter interaction at XUV photon energies, combined with the limited power of current XUV tabletop sources, hamper their disruptive potential for ultrafast spectroscopy and extreme nonlinear optics. Moreover, the high absorption in this frequency range forbids the focusing of XUV radiation with a transmissive objective, preventing focusing at the diffraction limit by nanometer wavelength radiation.

Radiation–matter interaction can get enhanced by plasmonic nanostructures thanks to the field enhancement produced by plasmons, collective excitations of conduction electrons in metals, which play a key role in surface-enhanced infrared absorption (SEIRA) [30] and surface-enhanced Raman scattering (SERS) [31]. Both techniques (SERS and SEIRA) enable chemical sensing with sensitivity reaching the single-molecule detection limit [32–34] and have been adopted in several applications, e.g. pregnancy tests based on metal colloids and cancer screening [35]. Furthermore, physical systems supporting slow light [36–39] naturally enhance radiation–matter interaction. In particular, near-zero-index (NZI) media can slow down light propagation [40–43] enabling large optical nonlinearity [44], self-organization of frozen light [45], enhanced second and third harmonic generation [46] and active control of tunneling [47]. NZI materials can be artificially realized in the form of metamaterials [48–50] and can also naturally exist in the form of plasmas, transparent conductors, and metals near their bulk plasma frequency [51]. Thanks to their properties, NZI media are currently adopted in multiple photonic applications including sensing, guiding, vortex generation [52], trapping and emission of visible and infrared (IR) radiation [53].

Here we develop a method to localize XUV radiation at the nanometer scale by the exploitation of NZI heterostructures, focusing particularly on titanium–aluminum–titanium (Ti–Al–Ti) multilayers. Indeed, the NZI properties of Al and Ti for wavelength λ < 100 nm [51] indicate that such heterostructures can confine radiation over a length-scale of a few nanometers. By solving fully vectorial Maxwell's equations semi-analytically, we obtain the transcendent dispersion relations of several transverse-electric (TE) and transverse-magnetic (TM) plasmon polariton modes, which we solve numerically through a Newton–Raphson algorithm. We emphasize that the observed plasmon polariton modes are not traditional surface plasmon polaritons at the interface between a conducting material and a dielectric or in metal-dielectric multilayers [54, 55]. Conversely, they ensue from a complex interplay between total internal reflection and the spatially-structured absorption profile of the considered NZI heterostructure. We systematically analyze the confinement properties and the attenuation length of such modes, finding that radiation confinement can be efficiently manipulated by the Al thickness and that TM modes offer the best effective mode length for nonlinear XUV applications. Our results indicate that NZI index media constitute a promising platform to manipulate XUV radiation enhancing its localized interaction with matter, thus opening novel avenues for surface-enhanced XUV spectroscopies and extreme nonlinear optics applications.

We consider a Ti–Al–Ti heterostructure composed of two micron-sized Ti layers embedding a thin Al film with thickness $d\simeq$ 10–30 nm, see figure 1(a). Owing to the large thickness of the Ti layers compared to the XUV radiation wavelength $\lambda\simeq$ 10–100 nm, we approximate the Ti layers as semi-infinite volumes. We start our analysis from the curl equations $\nabla\times \textbf(\textbf,t) = \mu_0 \partial_t \textbf(\textbf,t)$ and $\nabla\times \textbf(\textbf,t) = - \partial_t \textbf(\textbf,t)$ for the time-dependent electric and magnetic induction fields $\textbf(\textbf,t)$ and $\textbf(\textbf,t)$ at the generic position r. In the linear isotropic response limit, the displacement vector $\textbf(\textbf,t)$ satisfies the constitutive relation $\textbf(\textbf,t) = \epsilon_0\int_^t \epsilon(t-t^,\textbf) \textbf(\textbf,t^) \mathrm dt^$, where $\epsilon(\tau,\textbf)$ is the spatially-modulated temporal response function. The dielectric permittivity profile $\epsilon(\omega,\textbf)$ is provided by the Fourier transform of $\Theta(\tau)\epsilon(\tau,\textbf)$, where $\Theta(\tau)$ is the Heaviside step function accounting for causality and ω is the radiation angular frequency. In the considered geometry, see figure 1(a), the dielectric permittivity profile is given by $\epsilon(\omega,\textbf) = \epsilon_}(\omega) \Theta_}(x) +$ $\epsilon_}(\omega) \Theta_}(x)$, where $\Theta_}(x) = \Theta(x+d/2) - \Theta(x-d/2)$, $\Theta_}(x) = \Theta(-x-d/2) + \Theta(x-d/2)$ and $\epsilon_}$ indicate the complex dielectric permittivities of Al/Ti materials, whose wavelength dependence is depicted in figure 1(b). Note that, in the XUV wavelength range $\lambda \simeq$ 10–100 nm, $|\epsilon^\prime_}|\lt 1$ (where $\epsilon^$ indicates the real part of epsilon) and both Al and Ti behave as NZI media [51].

Figure 1. (a) Sketch of the considered Ti–Al–Ti heterostructure, with Al thickness d, supporting plasmon polariton modes propagating over the z-direction. (b) Wavelength dependence of the complex dielectric permittivities $\epsilon_}$ (blue curves) and $\epsilon_}$ (red curves) [56, 57], where full/dashed curves indicate the real ($\epsilon^\prime_}$) / imaginary ($\epsilon^}_}$) parts of $\epsilon_}$.

Download figure:

Standard image High-resolution image

We seek monochromatic plasmon polariton modes with angular frequency $\omega = 2\pi c/\lambda$, where c is the speed of light in vacuum, propagating over the z direction and unbound over the y-direction, by taking the ansatz $\textbf(\textbf,t) = } \left[\textbf_0(x,z) \mathrm e^ \right]$ and $\textbf(\textbf,t) = } \left[\textbf_0(x,z)\mathrm e^ \right]$. Owing to the planar symmetry of the system, Maxwell's equations are split into two independent sets of equations for TE and TM modes, which enable to express the complex field vectors as the superpositions

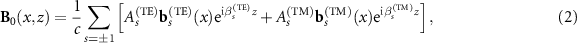
Equation (1)Equation (2)

where $s = \pm 1$ is a dimensionless index accounting for mode symmetry, $A^}_s$ are dimensional constants accounting for the arbitrary TE/TM mode amplitudes and $\textbf^}_s(x)$, $\textbf^}_s(x)$ are TE/TM dimensionless vector mode profiles with opposite reflection symmetry with respect to the y–z plane. Inserting the expressions above into Maxwell's equations and imposing boundary conditions for the continuity of By, Ez and Dx at the interfaces $x = \pm d/2$ together with the requirement that the field vanishes for $|x| \rightarrow +\infty$, we obtain the TM mode profiles

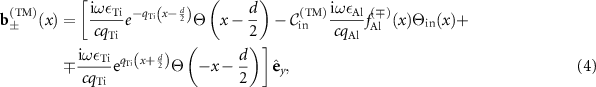
Equation (3)Equation (4)

where $\beta = \beta^}_$ represent the propagation constants of symmetric/antisymmetric plasmon polariton TM modes, $q_} = \sqrt}/c^2}$, $_}^} = (q_}\epsilon_} - q_}\epsilon_})\mathrm e^}d/2}/(q_}\epsilon_})$, $f^_}(x) = \frac\left(\mathrm e^}x} \pm \mathrm e^}x}\right)$ and $\beta = \beta^}_$ satisfies the TM dispersion relation

Equation (5)

Analogously, inserting equations (1) and (2) into Maxwell's equations and imposing boundary conditions for the continuity of Bx, Bz and Ey at the interfaces $x = \pm d/2$, we obtain the TE mode profiles

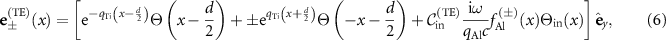
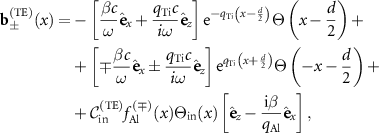
Equation (6)Equation (7)

where $\beta = \beta^}_$ represent the propagation constants of symmetric/antisymmetric plasmon polariton TE modes, $_}^} = [c(q_}- q_})/(\mathrm i\omega)]\mathrm e^}d/2}$ and $\beta = \beta^}_$ satisfies the TE dispersion relation

Equation (8)

Note that, while surface plasmon polaritons at a planar single-interface can only support TM polarization, NZI media heterostructures can also support TE modes, similarly to surface plasmon polaritons at metal–insulator–metal heterostructures [58]. We numerically solve equations (5) and (8) for every wavelength λ through a Newton–Raphson algorithm, obtaining the dispersion relations $\beta^}_$ of lowest order symmetric/antisymmetric plasmon polariton TE and TM modes, which are depicted in figures 2(a)–(d) for d = 30 nm. We emphasize that, although we find also higher-order modes in the considered Ti–Al–Ti heterostructure, they are highly lossy and we do not report them here. Furthermore we note that, while TE modes exist over all the considered XUV wavelength range, symmetric ($s = +1$) TM modes are cut-off within a specific spectral gap around $\lambda \simeq 50$ nm, see figure 2(d), owing to resonant absorption of Ti, see figure 1(b). Indeed, the resonant absorption peak of Ti (at $\lambda \simeq 30$ nm) produces refractive index dispersion in the surrounding spectral region owing to Kramers–Kronig relations. In particular, the real parts of $\epsilon_},\epsilon_}$ become identical at $\lambda_1 = 31$ nm and $\lambda_2 = 48$ nm, see figure 1(b). In turn, if one neglected absorption, guidance would have become strictly forbidden for all modes in the range 31 nm

View original article
JOURNAL OF PHYSICS-PHOTONICS

Comments (0)

No login
gif
format_indent_decrease