1 Introduction

A diverse range of stimuli from the external world is crucial for animal brains, not only to establish various perceptions and understand the real world (Hubel and Wiesel, 1968; Zhou et al., 2000; Pasupathy and Connor, 2002; Schmehl et al., 2024) but also to develop the neuronal circuits necessary to process this information (Ishikawa et al., 2014; Jenks and Shepherd, 2020). Environmental enrichment, which enhance the breeding environment for laboratory animals, improves the development of the cortical circuit for information processing while also suppressing brain dysfunction and anxiety disorders (Cancedda et al., 2004; Kempermann, 2019; Bibollet-Bahena et al., 2023). Previous studies have reported that enriched environment (EE) exposure exerts a broad range of effects on the brain, including enhanced activation (Sampedro-Piquero et al., 2015), modulation of interactions between cortical areas (Garbo et al., 2011), and improved cognitive capabilities (van Praag et al., 2020; Sale et al., 2009; Mainardi et al., 2010; Miranda et al., 2024). To understand the detailed neuronal mechanisms of information processing and devise methods to improve neuronal system dysfunction, it is crucial to comprehend how EE exposure, by increasing the variety of stimuli from the external world, modulates brain activities.

The primary visual cortex (V1) is one of the most well-studied targets of EE exposure (Bibollet-Bahena et al., 2023; Garbo et al., 2011; Kalogeraki et al., 2017). V1 microcircuits consist of a six-layered network structure, based on excitatory pyramidal (Pyr) neurons and inhibitory interneurons (Binzegger et al., 2004; Thomson and Morris, 2002; Thomson et al., 2002; Potjans and Diesmann, 2014). The superficial layers 2/3 (L2/3) in the layered microcircuit play a critical role in organizing visual perception and understanding the external world by integrating various neuronal signals, including feedforward inputs representing visual stimuli, feedback signals from higher visual areas, and horizontal projections from surrounding microcircuits (Gilbert and Wiesel, 1983; Self et al., 2013; van Kerkoerle et al., 2014). Prior studies have reported that the neural circuit in L2/3 of V1 is mainly constructed based on Pyr neurons and three subclasses of inhibitory interneurons: parvalbumin (PV), somatostatin (SOM), and vasoactive intestinal polypeptide (VIP). Recently, physiological and computational studies have begun to elucidate the details of the neural circuit structure and the interactions among these neuron classes and subclasses (Zhang et al., 2014; Neske et al., 2015; Mardinly et al., 2016; Cardin, 2018; Lee et al., 2017; Lee et al., 2018; Ito et al., 2024; Jiang et al., 2024). However, the characteristics and detailed mechanisms of modulation of neuronal activities in L2/3 of V1 through EE remain unclear.

In this study, we conducted a quantitative analysis to investigate the impact of the first exposure to EE, on neuronal responses in L2/3 of the mouse V1. EE alters the plasticity of the visual cortex through induction of immediate early genes (Montero, 1997; Cancedda et al., 2004; Piché et al., 2004). To identify the expression of immediate early genes following EE exposure, we conducted immunostaining for the immediate early gene product c-Fos (Sheng and Greenberg, 1990). We observed a significant increase in the number of neurons in L2/3 exhibiting high c-Fos fluorescence intensity under the EE exposure condition compared with those from mice under the standard housing (SH) condition. However, the number of neurons representing low c-Fos intensity did not significantly differ between the SH and EE exposure conditions. The characteristic modulation patterns observed in L2/3 of the mouse V1 through physiological experiments were reproduced by a cortical microcircuit model based on the biological architecture of L2/3 of the V1. These physiological and computational results indicated the modulatory effects of the switch from SH to EE on neuronal activities in L2/3 of the V1 and suggested the neural circuit structures responsible for inducing such modulation.

2 Materials and methods 2.1 Physiological experiments 2.1.1 Animal experiments and the switch from SH to EE

All experiments were performed in accordance with the guidelines of the National Institutes of Health (1996) and Japan Neuroscience Society and approved by Toho University Animal Care and Use Committee (Approval No. 22-519). C57BL/6N strain wild-type male mice (7 weeks old) were purchased from Japan SLC, Inc. Mice were housed in a conventional facility with a 12-h light/dark cycle (light period from 6:00 to 18:00), temperature of 22 ± 2°C, and free access to food and water in individual cages (W × D × H = 20 × 12.5 × 11.5 cm, Figure 1). Based on the protocol described in the previous study (Kawashima et al., 2009), the animals were kept for 2–3 days at a light intensity of 300 lux in the cage during the light period. The switch from SH to EE, EE exposure, was performed in different large cages (W × D × H = 64 × 44 × 34 cm, Figure 1) including a wider variety of objects between 9:00 and 15:00 for 90–180 min, with food and water available ad libitum, and the light inside the apparatus was adjusted to 300 lux. In contrast, mice that were individually housed in their home cages were designated as the SH group.

Figure 1. Experimental design to investigate the modulation of neuronal response in layers 2/3 (L2/3) of the primary visual cortex (V1) induced by the switch from standard housing (SH) to enriched environment (EE) exposure. Experimental procedures and design to measure neuronal activity in mouse L2/3 of V1. Mice housed in individual cages (20.0 × 12.5 × 11.5 cm) for 2–3 days were divided into the SH and EE exposure conditions. Under the EE exposure condition, in larger cages (64.0 × 44.0 × 34.0 cm), the mice were allowed to be active in an environment that enhances cognitive, physical, and social stimulation for 90–180 min.

2.1.2 Immunohistochemical staining

Mice were anesthetized and transcardially perfused with 4 mL of 25 mM phosphate buffered saline (PBS) chilled to 4°C and then with 50 mL of 2% paraformaldehyde (PFA) in 0.1 M phosphate buffer (PB) at a flow rate of 4.2 mL/min. After perfusion, brains were extracted and post-fixed in 2% PFA/PB at 4°C overnight. The brains were cryoprotected with 15% sucrose/PBS for 12 h, followed by 30% sucrose/PBS for 12 h. The brains were then embedded in OCT compound (Tissue-Tek) and coronal brain sections of 30 μm thickness were prepared using a microtome (REM-700, Yamato Kohki Industrial). Sections were collected at −3.16 mm from Bregma, referencing a brain atlas. The sections were washed three times in 25 mM PBS for 5 min each. After washing with PBS-T (PBS containing 0.3% Triton X-100), the sections were blocked in blocking buffer (5% normal goat serum/1% bovine serum albumin/0.3% Triton X-100 in PBS) at room temperature for 60 min. The sections were then incubated with rabbit anti-c-Fos antibody (1:1,000, 2,250, CellSignaling) in blocking buffer for 2 days at 4°C. Next, the sections were washed three times with PBS-T and then incubated with the secondary antibody (anti-rabbit Alexa-555 antibody (1:1,000, A-21429, Invitrogen) in 5% normal goat serum/PBS) for 2 h at room temperature. After three washes in PBS-T, the sections were stained with DAPI (1:1,500, D1306, Molecular Probes), washed twice more in PBS-T, fixed for 5 min in 4% PFA/PBS, followed by two final washes in PBS-T, and mounted using anti-fade mounting medium (mounting medium, vector). As described in a previous paper, among methods to detect immediate early genes, c-Fos antibodies are most widely used for immunohistochemical staining of mouse brain sections (Pompeiano and Colonnese, 2023).

2.1.3 Image acquisition and data analysis of neuronal responses in mouse V1

Confocal images of the brain tissue were obtained using a confocal laser microscope (LSM900 with Airyscan 2, Carl Zeiss) with a 20× objective lens (Plan-Apochromat NA 0.8). L2/3 of the V1 was defined as a region of interest (ROI) using DAPI fluorescence as an indicator, from which the number of DAPI-positive cells and the area of the analysis region were determined. Subsequently, we counted the number of c-Fos-positive cells within the ROI. In addition, we obtained the number of cells with high c-Fos fluorescence intensity (c-Fos-strong positive cells) from these images by subtracting the 2-fold background intensity from these images. To determine the number of cells with low c-Fos fluorescence intensity (c-Fos-weak positive cells), the number of c-Fos-strong positive cells was subtracted from the total number of c-Fos positive cells with c-Fos fluorescence intensity from these images by subtracting the background intensity from these images.

2.1.4 Statistical analyses of animal experiments

Quantitative data are represented as the median or mean ± standard error of the mean. Statistical analyses were conducted using Prism (GraphPad Software). A t-test was applied for comparisons between two groups.

2.2 Computational model and simulations 2.2.1 Cortical microcircuit model of L2/3 of V1

To investigate the neural mechanism of modulation by switching from SH to EE, we performed simulations of the cortical microcircuit model of L2/3 of V1, which was based on excitatory Pyr neurons and three subclasses of inhibitory interneurons (PV, SOM, and VIP). The network structure is illustrated in Figure 2A. The scale and structure of the model network were the same as those used in our previous computational study (Wagatsuma et al., 2023). This network structure was derived from prior circuit models reported by physiological and computational studies (Lee et al., 2017; Lee et al., 2018; Teramae et al., 2012; Pfeffer et al., 2013; Nobukawa et al., 2022). In the following section, we describe the essential elements of our microcircuit model. For a full description of our model, we refer the reader to our previous study (Wagatsuma et al., 2023).

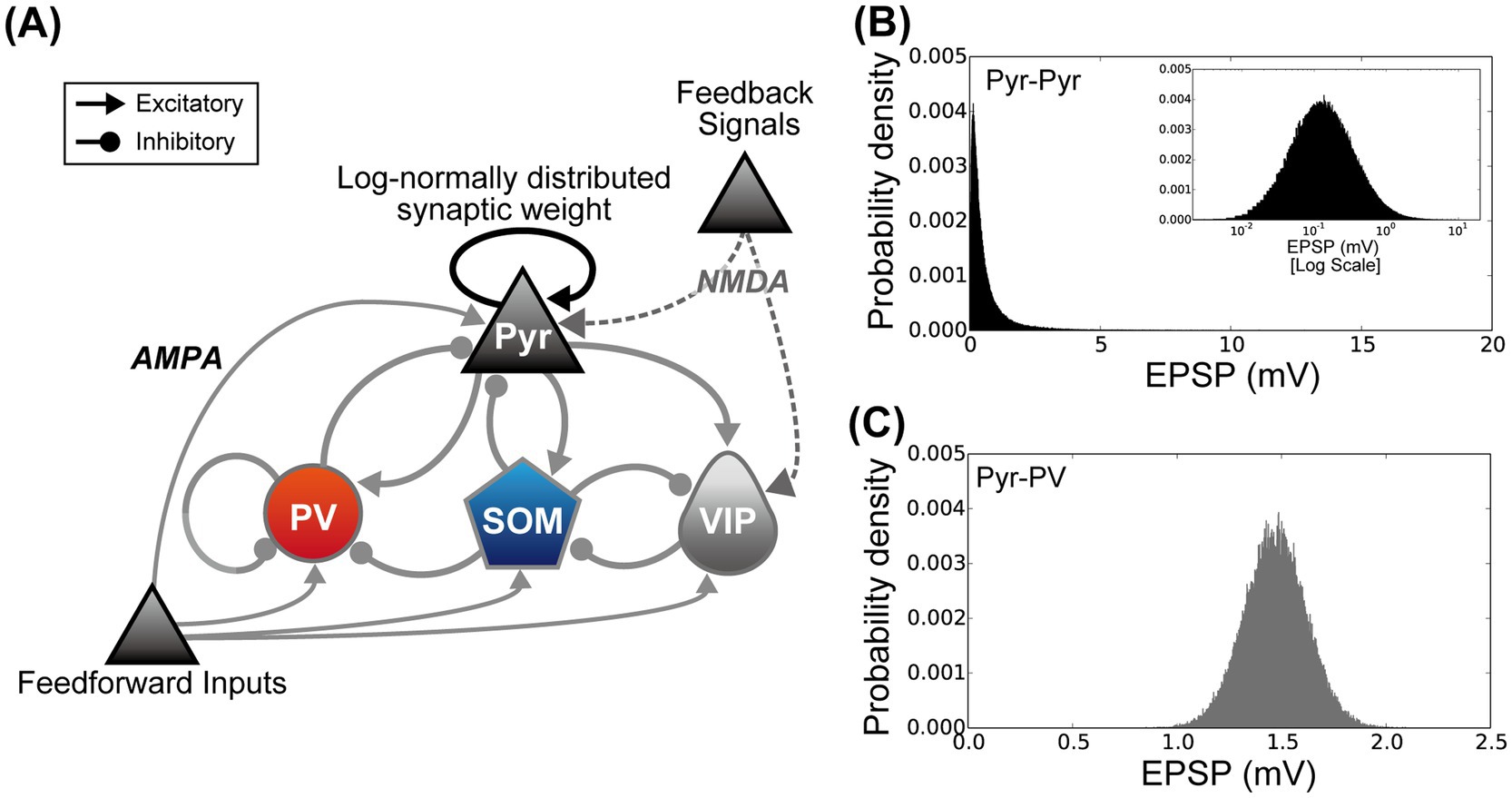
Figure 2. The microcircuit used to simulate the activity of layers 2/3 of the primary visual cortex under the standard housing and enriched environment exposure conditions. (A) Architecture of the proposed cortical microcircuit model. The model network was designed according to our prior computational model (Wagatsuma et al., 2023). Triangular and circular arrowheads represent excitatory and inhibitory connections, respectively. Connections between pyramidal (Pyr) model neurons (black triangular arrowheads) indicate that synaptic connections are distributed according to a log-normal distribution. The synaptic weights of other connections obeyed a Gaussian distribution (gray triangular and circular arrowheads) (Song et al., 2005; Lefort et al., 2009; Teramae et al., 2012). (B) The distribution of synaptic weights among Pyr model neurons. Excitatory postsynaptic potentials from Pyr to Pyr model neurons follow a log-normal distribution [black triangular arrowheads in the panel (A)]. The inset graph is a plot of the same distribution using a log scale for the x-axis. (C) Example distribution of synaptic weights from Pyr model neurons to model inhibitory interneurons (from Pyr to parvalbumin (PV) populations). In contrast to connections between Pyr model neurons, the synaptic weights from excitatory to inhibitory, inhibitory to inhibitory, and inhibitory to excitatory neurons are distributed according to a Gaussian distribution [gray triangular and circular arrowheads in the panel (A)].

The full network of our model consisted of approximately 2,650 integrate-and-fire model neurons (2,068 Pyr, 268 PV, 175 SOM, and 140 VIP neurons) and approximately 900,000 model synapses. These were determined according to previous computational studies (Potjans and Diesmann, 2014; Lee et al., 2017). The number of synapses was determined according to the connection probability (see Wagatsuma et al., 2023 for details). The dynamics of the membrane potential (V) of integrate-and-fire model neurons were determined by the following equation:

dVtdt=−Vt−Elτm+IPyrt+IPVt+ISOMt+IVIPt+IexttCm,    (1)

where the membrane time constant, τm, was chosen depending on the neuron class and inhibitory interneuron subclass. In this study, we used 10.5, 3.1, 11.8, and 10.9 ms for Pyr neurons and PV, SOM, and VIP interneurons, respectively. In contrast, the membrane capacitance, Cm, was set to 200 pF irrespective of the neuron class or subclass. The leak reversal potential was El=−70mV.

The synaptic currents, IPyr(t), IPV(t), ISOM(t), and IVIP(t), flowing into the model neuron from Pyr neurons and the PV, SOM, and VIP interneuron subclasses were determined by the following equation (Buehlmann and Deco, 2008; Deco and Thiele, 2011; Wagatsuma et al., 2022; Wagatsuma et al., 2023):

Isynt=gjsynVt−VNC∑jsjsynt,    (2)

where VNC indicates the reversal potential depending on the model neuron class. We used VNC=0mV for IPyr(t) for the excitatory synaptic current. To implement inhibitory synaptic currents for IPV(t), ISOM(t), and IVIP(t), VNC was set to −70 mV. The conductance strength of the fully activated synapse, gsyn, was determined by classes and subclasses of pre- and postsynaptic neurons. In this study, the strength and the distribution of gsyn were chosen according to our prior computational model (Wagatsuma et al., 2023). The gsyn strengths among Pyr neurons were determined using a log-normal distribution (Figure 2B) (Song et al., 2005; Lefort et al., 2009; Teramae et al., 2012; Nobukawa et al., 2022), whereas other synaptic connections obeyed a Gaussian distribution (Figure 2C). The mean and variance for the gsyn strengths were the same as those used in our prior computational study (Wagatsuma et al., 2023). sjsyn represented the fraction of open channels from the j-th model neuron, which was computed as:

dsjsyndt=−sjsyntτsyn+∑kδt−tjk−dj,    (3)

where τsyn represents the time constant for the post-synaptic decay, which was determined by the connections from pre- and post-synaptic neuron classes (Pfeffer et al., 2013; Lee et al., 2018; Wagatsuma et al., 2023). The sum over k ran over all spikes from connecting presynaptic model neurons. Each spike was represented by a Dirac delta function, δt, which assumes a nonzero value at the spike times (tjk) of the presynaptic neurons (and zero at all other times) and integrates to one over any interval encompassing tjk. dj is the delay from the j-th presynaptic neuron. The synaptic delay from the j-th presynaptic neuron, dj, was determined by a Gaussian distribution with a mean of 2.0 ms and a variance of 0.2 ms for excitatory connections and a mean of 1.0 ms and a variance of 0.1 ms for inhibitory connections. These means and variances for the inhibitory synaptic delay were applied irrespective of the interneuron subclass.

Iext(t) in Equation 1 represents the synaptic currents of external inputs to model neurons. Our model received three types of external inputs: background inputs to induce spontaneous activity, feedforward inputs from the retina, and feedback signals from higher visual cortices such as V2 and V4. These external inputs were given by independent Poisson spike trains. All model neurons received the background inputs. Feedforward inputs were directed to their target model neuron populations, selected randomly based on the connection probabilities. The background and feedforward inputs were mediated by AMPA type glutamatergic receptors. In contrast, feedback signals were projected to Pyr neuron and VIP interneuron populations, which were given by NMDA receptor-mediated synaptic currents. These feedforward inputs driven by the AMPA and feedback signals given by NMDA receptors were consistent with previous physiological studies of V1 (Self et al., 2012; Herrero et al., 2013). Additionally, previous computational studies have suggested that feedback signals mediated by NMDA synapses contribute to the modulation of both neuronal activity and the synchronization of responses in the visual cortex (Wagatsuma et al., 2016; Wagatsuma et al., 2021). The populations used to represent these feedforward inputs and feedback signals both consisted of 100 Poisson spike neurons. The connection probability for feedforward inputs was determined according to our prior computational model (Wagatsuma et al., 2023). The connection probability from feedback signals to the populations of Pyr neurons and VIP interneurons were 0.075 and 0.05, respectively.

The synapses used to model the external inputs in this study were the same as those used by our prior computational model (Wagatsuma et al., 2023). The AMPA type glutamatergic receptors mediating background and feedforward inputs were defined as:

IAMPAt=gjAMPAVt−VE∑jsjAMPAt,    (4)

where gAMPA is the conductance of the fully activated synapse for background or feedforward inputs. VE = 0 mV represents the reversal potential of the excitatory synapse. The fraction of open channels of model neurons from the j-th Poisson spike train (sjAMPA) was determined as:

dsjAMPAdt=−sjAMPAtτAMPA+∑kδt−tjk−dj,    (5)

where the postsynaptic-decay time constant for background and feedforward inputs is τAMPA = 2.0 ms, irrespective of the class of target neuron.

In this study, we used a standard computational model for generic NMDA receptors (Wang, 1999), where the NMDA-receptor mediating synaptic current, INMDA, was defined as follows:

INMDAt=gjNMDAVt−VE1+Mg2+exp−0.062Vt/3.57∑jsjNMDAt,    (6)

where gNMDA is the synaptic conductance of a fully open NMDA synapse. [Mg2+] = 1 mM represents a voltage-dependent block of NMDA channels (Jahr and Stevens, 1990). The fraction of open NMDA channels in a synapse is sjNMDA, which was calculated as:

dsjNMDAtdt=−sjNMDAtτNMDA,decay+αxt1−sjNMDAt,    (7) dxtdt=−xtτNMDA,rise+∑kδt−tNMDAk,    (8)

where α = 1/ms. The rise time for an NMDA synapse is τNMDA,rise = 2 ms, and their decay time constant is τNMDA,decay = 100 ms (Buehlmann and Deco, 2008; Wagatsuma et al., 2023). The sum over k is over spike time (tNMDAk), which, here, is the times at which spikes occur in the Poisson spike train representing the feedback signals.

The experimental conditions for SH and EE exposure were determined by the strengths of feedforward inputs and feedback signals. Under the EE exposure condition, a wider variety of visual objects were projected onto the animals’ visual field to activate neurons across different levels of the visual cortex compared with that in the SH condition. Furthermore, EE exposure may enhance interactions between animals and objects within their home cage, as well as increase locomotion in animals. We speculated that under the EE exposure condition, both feedforward inputs and feedback signals are more actively projected onto the cortical microcircuit in V1 than those under the SH condition. In this study, to simulate the SH condition, we employed Poisson spike trains of 10 Hz for the feedforward inputs and 5 Hz for the feedback signals. Conversely, in the EE exposure condition, the firing rate of the feedforward inputs was increased to 20 Hz. Similarly, the neurons representing the feedback signals in the EE exposure condition exhibited a firing frequency of 10 Hz.

2.2.2 Computational simulations and numerical experiments of our proposed model

The differential equations presented in Equations 1–8 were integrated by employing a fourth-order Runge–Kutta algorithm with a time step of 0.1 ms. The simulation code was written in the C programing language.

To investigate the mechanism of modulation by the switch from SH to EE, we performed simulations of the proposed microcircuit model using external inputs mimicking the SH and EE exposure conditions. As shown previously, these conditions were determined by the strengths of the feedforward inputs and the feedback signals. We conducted 10 trials of the model simulations, each lasting 60 biological seconds, under these conditions. The simulation length and the number of trials were determined based on the scale of the model network and computational cost constraints.

2.2.3 Data analysis of microcircuit model responses

To relate the activities of our cortical microcircuit model to the neuronal responses experimentally observed in L2/3 of the mouse V1, we computed the firing rates of individual Pyr model neurons under both the SH and EE exposure conditions. In this study, we assumed that Pyr model neurons with a firing rate ranging from 1.5 to 3.0 Hz correspond to c-Fos-weak positive cells (weak positive Pyr). In contrast, Pyr model neurons exhibiting a firing rate exceeding 3.0 Hz were classified as c-Fos-strong positive cells (strong positive Pyr). In addition, we computed the ratios of weak and strong positive Pyr neurons within the population of Pyr model neurons to relate to the neuronal responses in L2/3 of the mouse V1 to the activities of our model. For the statistical analysis, we applied a t-test to the responses of Pyr model neurons, following to the animal experiments.

3 Results 3.1 Modulation of neurons in L2/3 of the mouse V1 induced by the switch from SH to EE

We physiologically and computationally investigated and analyzed the impacts of the switch from SH to EE on modulation of neuronal responses in L2/3 of the mouse V1 (Figure 1). c-Fos is the protein product of the immediate early gene c-Fos and a marker of neuronal activation in layers 2/3 neurons of the mouse V1 (Nguyen et al., 2015; Pizzo et al., 2016). Its expression reaches its peak approximately 90 min after neuronal activity (Morgan and Curran, 1991; Sheng and Greenberg, 1990) and remains elevated above baseline levels until 180 min after neuronal activity (Zangenehpour and Chaudhuri, 2002). Mice were exposed to EE, and immunohistochemical staining for c-Fos, was performed 90 to 180 min (Figure 3A) after the switch from SH to EE.

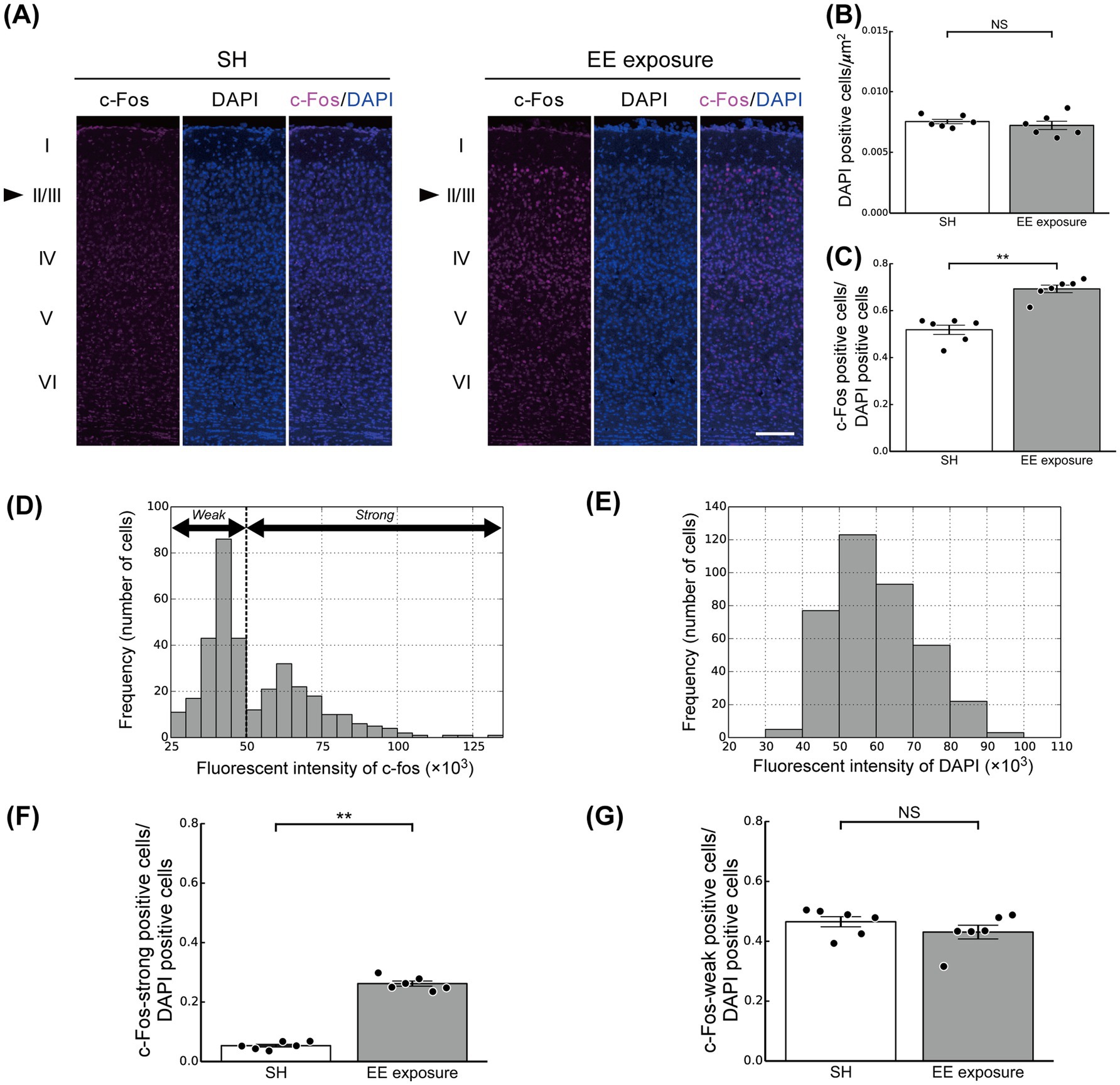
Figure 3. Enriched environment (EE) exposure-induced modulation of the ratios of c-Fos-positive cells in layers 2/3 (L2/3) of the mouse primary visual cortex (V1). (A) Representative images of coronal sections of V1 under the standard housing (SH) (left panel) and EE exposure (right panel) conditions. The sections were stained with a c-Fos antibody (left) and DAPI (center) in each panel. Neuronal response was determined by the fluorescence intensity. Arrowheads indicate L2/3. Scale bars, 100 μm. (B) The ratio of DAPI-positive cells in L2/3 of the mouse V1 under the SH (white bar) and EE exposure (gray bar) conditions. (C) Ratios of c-Fos-positive cells in L2/3 of the mouse V1 under the SH and EE exposure conditions. (D) The distribution of c-Fos fluorescence intensity. (E) The distribution of DAPI fluorescence intensity. (F) Ratio of c-Fos-strong positive cells. (G) Ratio of c-Fos-weak positive cells. Black dots represent the responses of individual animals. Error bars represent the standard error of the mean. Asterisks indicate significant differences between the two conditions (t-test, **p < 0.01, NS, not significant).

Quantification of cells in L2/3 of V1 using DAPI staining (nuclear staining; the center panel in Figure 3A) revealed no difference in the number of cells per unit area between the SH and EE exposure groups (t-test, p = 0.47; Figure 3B). To further investigate the impact of the switch from SH to EE on modulation of neuronal responses, we analyzed the number and distribution of c-Fos-positive neurons in L2/3 of V1 under both the SH and EE exposure conditions (Figures 3C,D). In this study, c-Fos positive cells were identified based on c-Fos fluorescence intensity that was higher than the background intensity (see also the Materials and Methods section for details). We used the fluorescence intensity as the metric for the neuronal responses. The distributions of c-Fos and DAPI fluorescence intensities were shown in Figures 3D,E. Calculation of the number of c-Fos-positive neurons in the L2/3 area of V1 showed an increased number in the EE exposure condition compared with that of the SH condition (t-test, p < 0.01; Figure 3C).

We further found that c-Fos-positive neurons could be divided into groups with high and low c-Fos fluorescence intensity (Figure 3D). For a more detailed analysis of the neuronal modulation induced by EE exposure, neurons with c-Fos fluorescence intensity more than twice that of the background of tissue sections were classified as neurons with high c-Fos fluorescence intensity (c-Fos-strong positive cells). In contrast, to determine the number of neurons with low c-Fos fluorescence intensity (c-Fos-weak positive cells), we subtracted the number of c-Fos-strong positive cells from the total number of c-Fos-positive cells (see also the materials and methods section for details). This threshold, defined as a c-Fos fluorescence intensity exceeding twice the background level, effectively distinguished c-Fos-strong positive cells from c-Fos-weak positive cells (Figure 3D). In contrast, no such characteristic was observed in the fluorescence intensity distribution of DAPI (Figure 3E). Then, we calculated the ratios of the c-Fos-strong and c-Fos-weak positive cells under both the SH and EE exposure conditions relative to the total number of DAPI positive cells, and the results are summarized in Figures 3F,G, respectively.

The number of c-Fos-strong positive cells under the EE exposure condition was significantly greater than that under the SH condition (t-test, p < 0.01; Figure 3F), implying that L2/3 neurons in V1 were activated by the EE exposure. However, in contrast, there was no significant difference in the ratio of c-Fos-weak positive cells between the EE exposure and SH conditions (t-test, p = 0.30; Figure 3G). These physiological findings imply a characteristic modulation pattern in L2/3 of V1 induced by the switch from SH to EE: a significant increase in the number of highly activated neurons occurs from the SH to EE exposure conditions, while the proportion of weakly activated neurons remains constant regardless of the condition. By obtaining these observations, in order to explore the potential physiological mechanisms of EE exposure, we next aimed to develop and simulate a computational microcircuit model based on the biologically plausible structure of L2/3 of the visual cortex.

3.2 Responses of the cortical microcircuit model to simulations mimicking the SH and EE exposure conditions

To understand the possible mechanism of EE-exposure-induced neuronal modulation in L2/3 of the mouse V1, we performed simulations using a microcircuit model with a biologically plausible L2/3 network of V1 (Figure 2A) (Wagatsuma et al., 2023). The fundamental structure and network of our microcircuit model are described in the Materials and Methods section. This microcircuit model of L2/3 in V1 incorporated excitatory Pyr neurons and three inhibitory interneuron subclasses: PV, SOM, and VIP. In the proposed network, synaptic strengths among Pyr neurons were characterized by a long-tailed, log-normal distribution (Figure 2B) (Song et al., 2005; Lefort et al., 2009; Teramae et al., 2012). Other synaptic connections obeyed a Gaussian distribution (Figure 2C).

In this study, the experimental conditions for SH and EE exposure were distinguished based on the strengths of the feedforward inputs originating from the retina and the feedback signals derived from higher visual areas. Feedforward inputs mediated by AMPA type glutamatergic receptors were applied to all classes and subclasses of the model neuron population, whereas the feedback signals applied by the NMDA receptor-mediating synaptic currents were projected onto the Pyr model neuron and VIP model interneuron populations (Figure 2A). To simulate the SH condition, we applied Poisson neuron populations with frequencies of 10 Hz and 5 Hz as the feedforward inputs and feedback signals, respectively, to our model. To simulate the EE exposure condition, the feedforward and feedback signals were set to 20 Hz and 10 Hz, respectively.

Figure 4A shows the spike raster plots of Pyr model neurons and the three subclasses of inhibitory interneurons in the SH condition. In this simulation, we applied feedforward inputs starting at 100 ms and feedback signals starting at 200 ms. These external inputs to the model markedly modulated the activities of all neuron classes and subclasses from the spontaneous condition. The spike raster for the EE exposure condition is presented in Figure 4B. Under this condition, Pyr model neurons and PV and SOM inhibitory interneurons seemed to be more activated than in the SH condition, likely because of the increases in the rates of feedforward inputs and feedback signals. In addition, the responses of the microcircuit model with these feedforward inputs and feedback signals remained stable even during prolonged simulation durations.

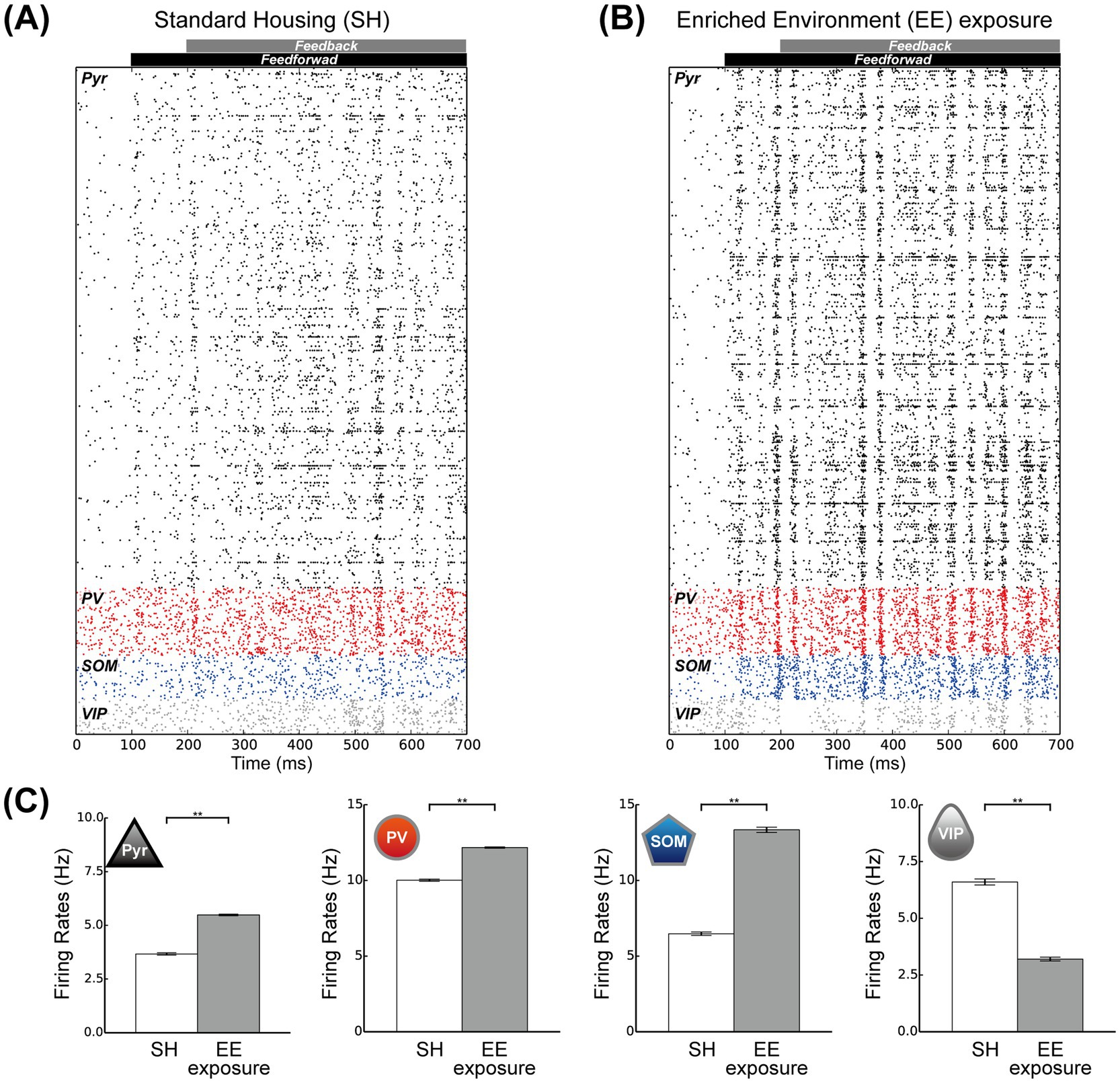
Figure 4. Responses of the proposed microcircuit model. (A) Raster plots for the standard housing (SH) condition for all spike trains of the pyramidal (Pyr), parvalbumin (PV), somatostatin (SOM), and vasoactive intestinal polypeptide (VIP) neuron populations for 700 ms. (B) Raster plots with respect to the enriched environment (EE) exposure condition for all spike trains of the Pyr, PV, SOM, and VIP neuron populations for 700 ms. (C) The mean population firing rates of Pyr, PV, SOM, and VIP neurons for the SH (white) and EE exposure (gray) conditions (10 simulation trials). The error bars indicate the standard error. Asterisks indicate significant differences between the two conditions (t-test, **p < 0.01).

To analyze the responses of our microcircuit model, we simulated our network model under these two conditions, performing 10 trials of 60 biological seconds for each condition, and computed the population rates for Pyr model neurons and the three subclasses of inhibitory model interneurons (Figure 4C). The population activities of Pyr model neurons and PV and SOM inhibitory model interneurons were significantly enhanced under the EE exposure condition compared with those under the SH condition (t-test, p < 0.01). Conversely, the population activities of the VIP model interneuron subclass significantly decreased from the SH to the EE exposure condition (t-test, p < 0.01). These results implied that the responses of our microcircuit model are dependent on the strengths of the feedforward inputs and feedback signals. Specifically, enhancement of these external inputs significantly activated the Pyr model neuron population, consistent with the effects of the switch from SH to EE observed in our experiments, as shown in Figure 3A.

Our physiological experiments revealed characteristic modulation patterns in L2/3 of V1 induced by switching from SH to EE (Figure 3). To relate the responses of our microcircuit model to our physiological observations, we computed the firing rates of individual Pyr model neurons under both the SH and EE exposure conditions. The distributions of firing rates of individual Pyr model neurons under the SH and EE exposure conditions are presented in Figures 5A,B, respectively. In the EE exposure condition, enhancements in feedforward inputs and feedback signals resulted in a rightward shift of the median value compared with those in the SH condition, as indicated by triangles in Figures 5A,B. Furthermore, the number of Pyr model neurons with firing rates ranging from 0 to 2 Hz in the EE exposure condition was less than that in the SH condition. These results implied a marked increase in highly activated Pyr model neurons under the EE exposure condition compared with that in the SH condition, and this characteristic is similar to that observed in our physiological observations.

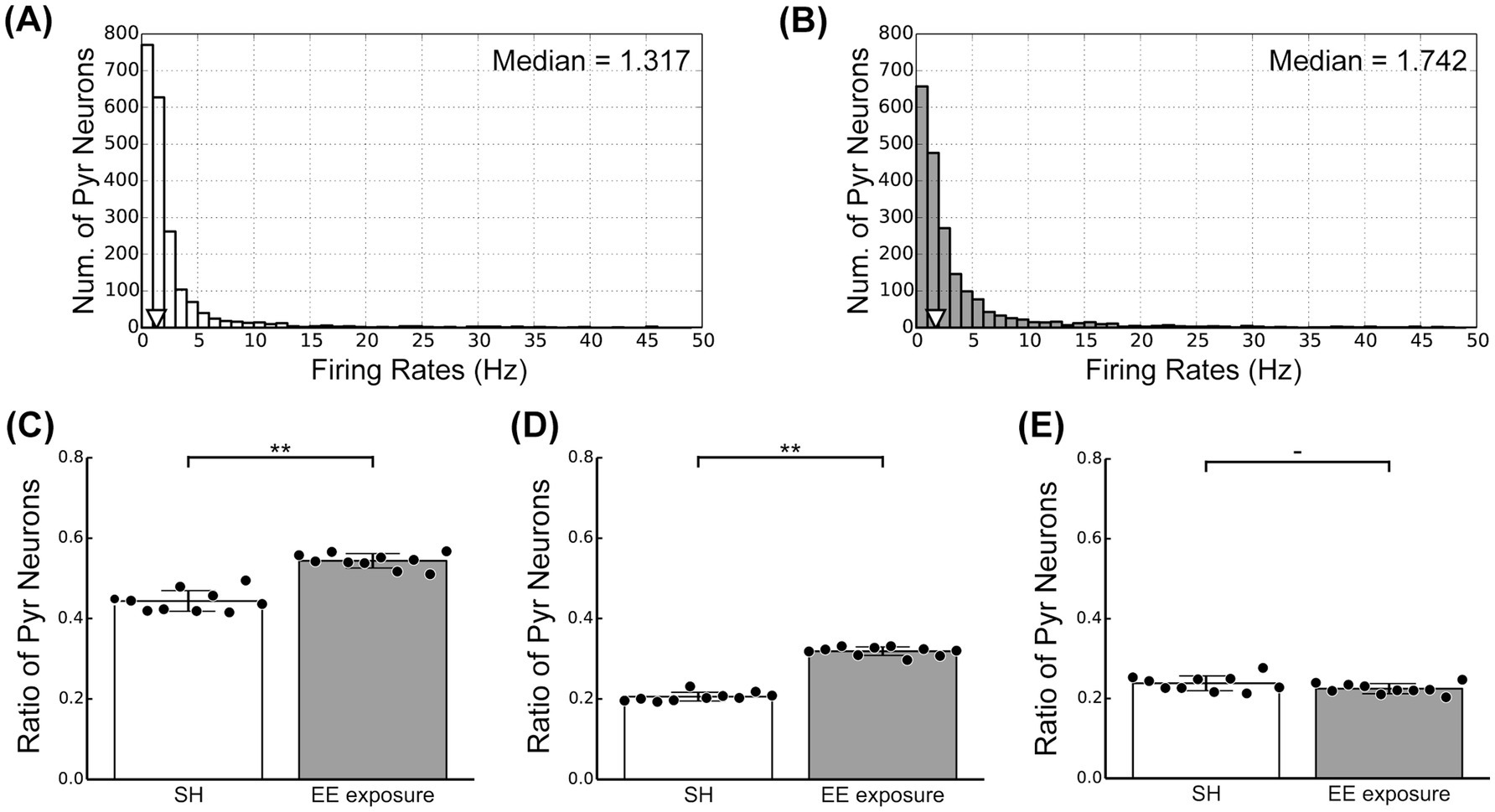
Figure 5. Activity of excitatory pyramidal (Pyr) model neurons in the standard housing (SH) and enriched environment (EE) exposure conditions. (A) The distribution of firing rates of Pyr neurons under the SH condition. (B) The distribution of firing rates of Pyr neurons under the EE exposure condition. (C) Ratio of positive Pyr model neurons with firing rates exceeding 1.5 Hz within the Pyr population. (D) Ratio of strong positive Pyr model neurons with firing rates exceeding 3.0 Hz. (E) Ratio of weak positive Pyr model neurons with a firing rate ranging from 1.5 to 3.0 Hz. Asterisks indicate significant differences between the two conditions (t-test, **p < 0.01, -p < 0.1).

To further analyze the responses of our microcircuit model, we assumed that Pyr model neurons with a firing rate ranging from 1.5 to 3.0 Hz correspond to c-Fos-weak positive cells (weak positive Pyr neurons). The threshold firing rate to distinguish weak positive from inactivated Pyr neurons was based on approximately twice the spontaneous population activity of Pyr neurons (0.6 Hz). In contrast, we classified Pyr model neurons with firing rates exceeding 3.0 Hz as c-Fos-strong positive cells (strong positive Pyr neurons). We computed the ratios of weak and strong positive Pyr neurons within the Pyr model neuron population to compare physiological activities in L2/3 of the mouse V1, as shown in Figure 3, with the responses generated by our model. The ratio of positive Pyr model neurons with firing rates exceeding 1.5 Hz within the Pyr population is presented in Figure 5C. Furthermore, we display the ratios of strong and weak positive Pyr neurons within the Pyr model neuron population in Figures 5D,E, respectively. The EE exposure condition significantly increased the ratio of positive Pyr model neurons, as well as the ratio of strong positive Pyr model neurons, compared with the SH condition (t-test, p < 0.01; Figures 5C,D). However, there was no significant difference in the ratio of weak positive Pyr neurons between the SH and EE exposure conditions (t-test, p = 0.09; Figure 5E). These modulation patterns generated by our model were statistically in good agreement with the patterns of neuronal response observed in our physiological experiments depicted in Figure 3.

The population activities of PV and SOM inhibitory model interneurons, as well as Pyr model neurons, significantly increased from the SH to the EE exposure condition (Figure 4C). To gain deeper insights into the model’s responses, we analyzed the firing rates of individual PV and SOM interneurons under both SH and EE exposure conditions (Supplementary Figures S1A–D). Regardless of the simulation conditions, the firing rate distributions of individual PV and SOM model interneurons exhibited characteristics similar to those observed in the Pyr population (Figures 5A,B). Furthermore, we computed the ratios of weak and strong positive model neurons within the Pyr, PV, and SOM model populations with respect to both SH and EE exposure conditions (Supplementary Figures S1E,G). In these analyses, the firing rate thresholds were consistent with those applied in our previous analyses presented in Figures 5C–E. The modulation patterns observed in the ratios of positive, strong-positive, and weak-positive model neurons within these populations were statistically consistent with those observed in our physiological experiments.

3.3 Analyses of the threshold for distinguishing between weak and strong positive Pyr model neurons

We analyzed the ratios of weak and strong positive Pyr neurons within the Pyr model neuron population (Figure 5) to relate the neuronal responses physiologically observed in L2/3 of the mouse V1 (Figure 3). In our analyses, Pyr model neurons with firing rates from 1.5 to 3.0 Hz were classified as c-Fos-weak positive, while those with rates exceeding 3.0 Hz were categorized as c-Fos-strong positive. However, the results of these analyses depended on the threshold set for the firing rate used to distinguish between positive and negative (inactive) Pyr model neurons. To further analyze the responses of our model, we reanalyzed the ratios of weak and strong positive Pyr model neurons while varying the thresholds for weak positive Pyr neurons, with firing rates ranging from 1.0 to 2.0 Hz, 1.5 to 3.0 Hz, and 2.0 to 4.0 Hz, as functions of feedforward and feedback frequencies. For this analysis, we performed 50 simulation trials with a length of 6 biological seconds by systematically adjusting the rates of these two inputs. The means of feedforward inputs and feedback signals were systematically varied in the range from 0 to 30 Hz, in steps of 5 Hz.

Figure 6 summarizes the ratios of positive, strong positive, and weak positive Pyr model neurons within the Pyr neuron population using weak positive thresholds ranging from 1.5 to 3.0 Hz (Figure 6A), 1.0 to 2.0 Hz (Figure 6B), and 2.0 to 4.0 Hz (Figure 6C). These ratios are presented as functions of feedforward and feedback signal frequencies. In each panel of Figure 6, cells outlined with white and black borders represent the ratios from simulations under our SH and EE exposure conditions, respectively. Irrespective of the threshold level, the ratios of positive Pyr model neurons monotonically increased with increases in both feedforward inputs and feedback signals, as shown in the left column of Figure 6. This trend was common for observations of strong positive Pyr model neurons (center column in Figure 6). These results are consistent with the physiologically observed significant increase in the ratios of c-Fos-positive and strong positive neurons in L2/3 of V1 induced by the switch from SH to EE (Figures 3C,F).

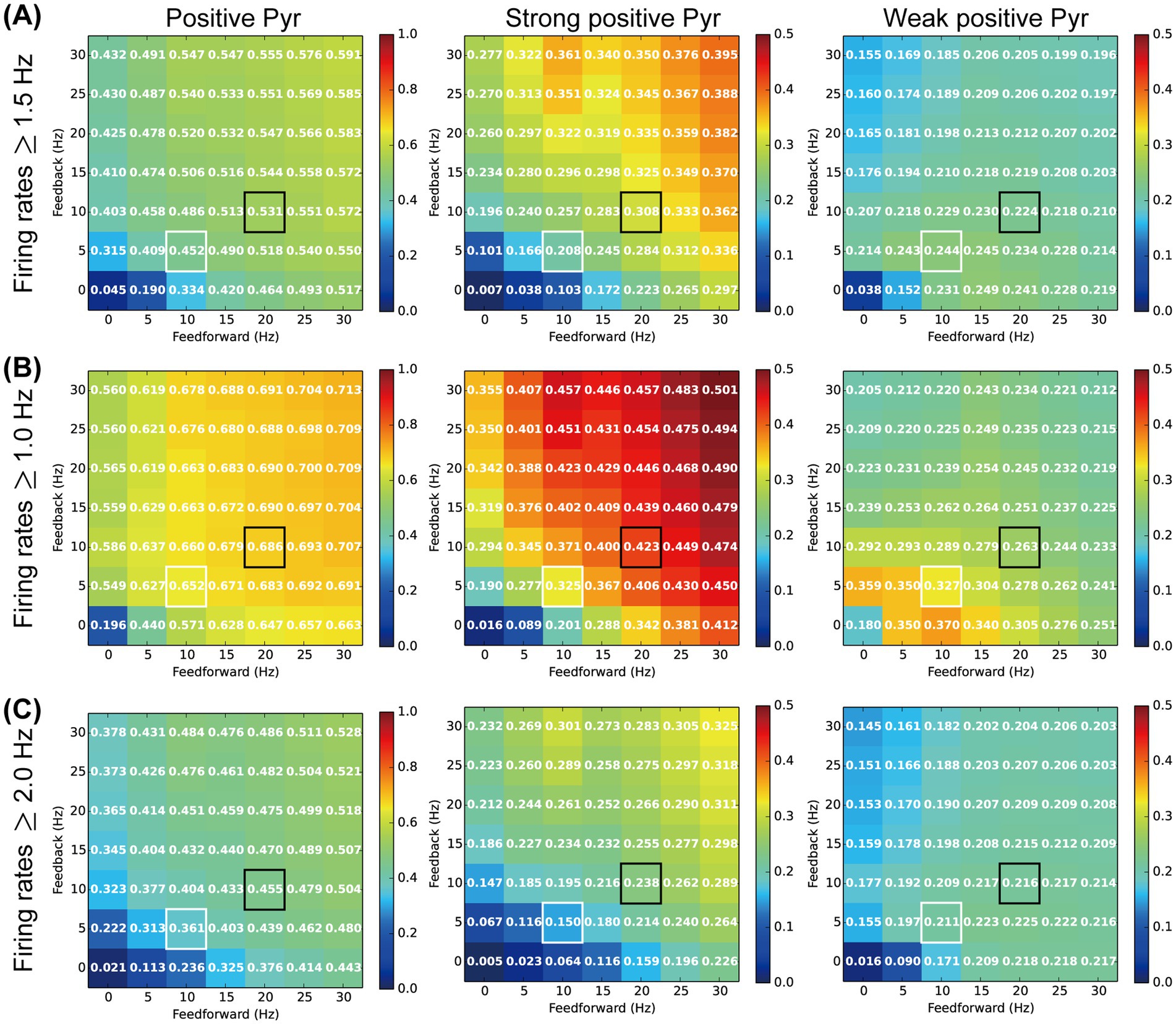
Figure 6. Influences of the inputs and threshold on our analyses. The colors and values of the cells in the matrix represent the ratio of activated pyramidal (Pyr) model neurons. The x- and y-axes indicate firing rates of feedforward and feedback inputs to our model, respectively. Cells with white and black borders in each panel correspond to the standard housing and enriched environment exposure conditions of our model simulations, respectively. (A) Ratio of c-Fos-positive Pyr model neurons based on a firing rate threshold of 1.5 Hz. The left, middle, and right panels indicate the ratios of c-Fos-positive (≥1.5 Hz), strong positive (>3.0 Hz), and weak positive (1.5–3.0 Hz) Pyr model neurons, respectively. (B) Ratio of c-Fos positive Pyr model neurons based on a firing rate threshold of 1.0 Hz. The left, middle, and right panels indicate the ratios of c-Fos-positive (≥1.0 Hz), strong positive (>2.0 Hz), and weak positive (1.0–2.0 Hz) Pyr model neurons, respectively. (C) Ratio of c-Fos-positive Pyr model neurons based on a firing rate threshold of 2.0 Hz. The left, middle, and right panels indicate ratios of c-Fos-positive (≥2.0 Hz), strong positive (>4.0 Hz), and weak positive (2.0–4.0 Hz) Pyr model neurons, respectively.

The ratios of weak positive Pyr model neurons were also influenced by the feedforward inputs and feedback signals, as well as by the threshold levels (right column in Figure 6). However, modulation of the ratio of weak positive Pyr model neurons by feedforward inputs and feedback signals was more moderate than that observed for the ratio of strong positive Pyr model neurons. In particular, across these three threshold levels, the decrease in the ratio of weak positive Pyr model neurons from the SH (white border) to EE exposure (black border) condition was substantially less than the increase observed in the ratio of strong positive neurons. This trend was consistent with our physiological observation that the switch from SH to EE does not significantly modulate the ratio of c-Fos-weak positive neurons in L2/3 of V1 (Figure 3G).

These results suggest that the ratios of weak and strong positive Pyr model neurons fluctuate depending on the threshold levels. However, the impact of feedforward inputs and feedback signals on the ratio of weak positive Pyr neurons was relatively moderate compared with their effect on strong positive Pyr neurons, particularly when weak positive thresholds were chosen to approximately twice or triple the spontaneous population activity of Pyr model neurons. Additionally, these thresholds appeared to be near the median of the distribution of firing rates in the Pyr model neuron population (Figures 5A,B). The potential mechanisms underlying these modulations, as suggested by our microcircuit model, will be discussed further in the Discussion section.

4 Discussion

In this study, we physiologically and computationally investigated the influences of the switch from SH to EE on responses in L2/3 of the mouse V1 (Figure 1). EE modulates plasticity within the visual cortex by inducing the expression of immediate early genes (Montero, 1997; Cancedda et al., 2004; Piché et al., 2004). Our physiological experiments employed immunostaining of the immediate early gene product c-Fo